算法与数据结构之排序（一）

最常用的排序算法：

冒泡排序、插入排序、选择排序、希尔排序、归并排序、快速排序、基数排序、桶排序。

时间复杂度

排序算法	时间复杂度
冒泡、插入、选择	O(n^2)
希尔	O(n1.5)
快排、归并	O(nlogn)
桶、基数	O(n)

1、桶排序（Bucket Sort）

桶排序 (Bucket sort)或所谓的箱排序，是一个排序算法，工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。简单来说就是要将排序的数据分到几个有序的桶里，再将每个桶里的数据进行单独排序。桶内排完序后，再把给桶里的数据按照顺序取出。

举个栗子！（将每个数据分到一个桶）😏😏

题目：我们需要将6个同学的分数（3，5，3，4，8，9）从大到小进行排序，满分为10分

首先我需要定义一个下界为11的数组a[11],初始化为零，表示这些分数还没有人得过。

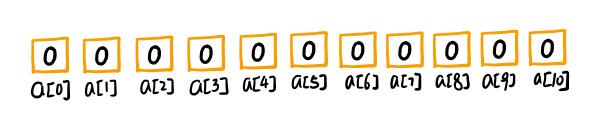
然后开始处理每一个人的分数

第一个同学分数为3分，则在相对应的a[3]的值基础上加1，a[3]的值从0变1,表示3分出现过一次。

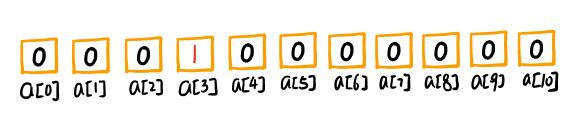
第二个人的分数为5，则在相对应的a[5]的值基础上加1，a[5]的值从0变1,表示5分出现过一次。

第三个人的分数为3，则在相对应的a[3]的值基础上加1，a[3]的值从1变2,表示3分出现了两次。

依此类推，最终结果为下图

最后我们将出现的分数打印出来，出现几次就打印几次

Java代码如下

import java.util.Scanner;
public class BucketSort {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        int n = scanner.nextInt(); //输入n个数
        int[] scores = new int[n];
        int[] bucket = new int[11];
        for (int i = 0; i < n; i++){ // 循环读入n个数，并进行桶排序
            scores[i] = scanner.nextInt();
            bucket[scores[i]]++; //进行计数，对应编号为scores[i]的桶放入分数
        }

        for (int i = 0; i < bucket.length; i++) {
            for (int j = 0; j < bucket[i]; j++) //出现几次就将桶的编号打印几次
                System.out.print(i + " ");
        }
    }
}

输入数据

1 2	6 3 5 3 4 8 9

输出数据

1	3 3 4 5 8 9

如果要实现从大到小排序，只需要将for (int i = 0; i < bucket.length; i++)改为for (int i = bucket.length; i > 0; i--)

桶排序就好比有11个桶🛢，编号从0~10.每出现一个数，就在对应编号的桶中放一个篮球🏀，最后只要数数每个桶中有几个篮球🏀就好啦！我们需要注意的是桶的数量

最后桶排序时间复杂度为O(M+N)，m为桶的个数，n为待排序数的个数。本次桶排序举的栗子是简化版的，真正的桶排序在分桶的时候，每个桶会有一个范围的数据，然后在桶里在进行排序。

2、冒泡排序（Bubble Sort）

冒泡排序的基本思想是：每次比较两个相邻的元素，如果它们的顺序错误就把他们交换过来。从第一个元素起。比较相邻的元素，如果第一个比第一个大，就交换。然后继续比较，知道最大的数到最后一个。所有元素重复以上动作。👈

举个例子，需要对数组a[5,8,3,4,2]进行从小到大排序

从小到大排序就需要将最大的数冒到最后面

int a[] = {5,8,3,4,2};
for (int i = 0; i < a.length - 1; i++){ // 5个数排序，只用进行n-1趟，即4趟
      for (int j = 0; j < a.length - 1 - i; j++){
          //从第1位开始比较直到最后一个归位的数，i可以认为为已经归位了几个数字
//第一趟 i = 0
第一次: 5 8 3 4 2 (j = 0)
第二次: 5 3 8 4 2 (j = 1)
第三次: 5 3 4 8 2 (j = 2)
第四次: 5 3 4 2 8 (j = 3) //8归位

//第二趟 i = 1
第一次: 3 5 4 2 8 (j = 0)
第二次: 3 4 5 2 8 (j = 1)
第三次: 3 4 2 5 8 (j = 2) //5归位

//第三趟 i = 2
第一次: 3 4 2 5 8 (j = 0)
第二次: 3 2 4 5 8 (j = 1) //4归位

//第四趟 i = 3
第一次: 2 3 4 5 8 (j = 0) //2归位

动态图如下：

Java代码如下

public class BubbleSort {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(); //输入n个数
        int[] scores = new int[n];
        for (int i = 0; i < n; i++)
            scores[i] = scanner.nextInt();

        // 冒泡排序核心部分
        for (int i = 0; i < n - 1; i++){ // n个数排序，只用进行n-1趟
            for (int j = 0; j < n - 1 - i; j++){ //从第1位开始比较直到最后一个归为的数，i可以认为为已经归为了几个数字
                if (scores[j] > scores[j + 1]){ // 比较大小并交换
                    int temp;
                    temp = scores[j];
                    scores[j] = scores[j + 1];
                    scores[j + 1] = temp;
                }
            }
        }
        for (int score : scores)
            System.out.print(score + " ");
    }
}

输入数据

1 2	10 8 9 14 2 90 76 46 35 24 57

输出数据

1	2 8 9 14 24 35 46 57 76 90

👉 冒泡排序的核心部分是双重嵌套循环。

👉 冒泡排序的时间复杂度为O(N^2)

3、快速排序（Qucik Sort）

快速排序基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。快速排序是基于一种“二分”思想，分治思想。

举个栗子，将4 1 6 2 9 3进行快速排序

首先在这个序列中随便找一个基准数（pivot）。为了方便，通常让第一个数4作为基准数。接下来，需要将这个序列所有比基准数大的数放在4的右边，比基准数小的数放在4的左边，即：

2 1 3 4 9 6

在初始状态下，数字4在序列的第一位。我们需要将4挪到中间的一个位置，假设这个位置是k。现在需要找这个k，并且以k为分界点，左边的数都小于等于4，右边的数都是大于等于4。

分别从初始序列“4 1 6 2 9 3”两端开始勘测。先从右往左找一个小于4的数，找到后，再从左往右找一个大于4的数，然后交换他们。这里可以用两个变量i和j，分别指向序列最左边和最右边。刚开始的时候“哨兵i”指向序列最左边（即i=1）,指向数字4，“哨兵j”指向序列最右边（即j=4）,指向数字3。

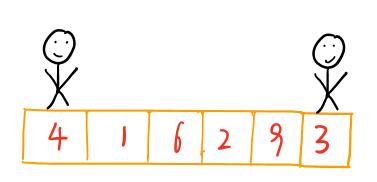
首先哨兵j开始出动。因为基准数设置为最左边的数。哨兵j一步一步向左挪到（即j–），直到找到一个小于4的数停下来，接下来哨兵i再一步一步向右挪动（即i++），直到找到一个大于4的数停下来。最后哨兵j停在了数字3上面，哨兵i停在了数字6上。

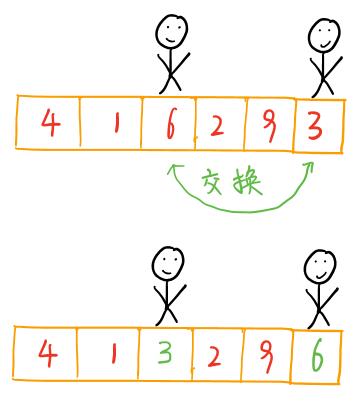
现在交换哨兵i和哨兵j所指向的元素的值。交换后序列如下

4 1 3 2 9 6

到此，第一次交换结束。接下来哨兵j继续向左挪动。哨兵j找到了数字2后，哨兵i继续向右挪动，然后与哨兵j相遇后，与基准数交换。第一轮勘测结束。此时4左边的数都小于等于4，4右边的数都大于等于4。哨兵j的使命就是要找小于基准数的数，而哨兵i的使命就是找大于基准数的数，直到i和j相遇为止。

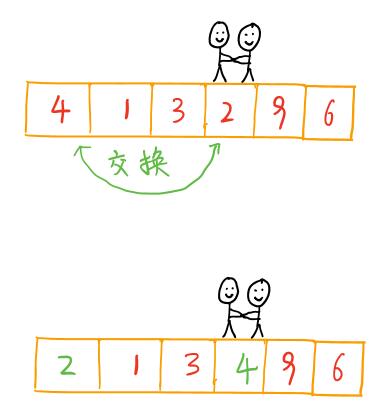
相遇后与基准数交换后的序列为：

2 1 3 4 9 6

现在基准数4已经归位，此时，我们以4为分界点拆分为两个序列，左边为“2 1 3”，右边序列为“9 6”。接下来我们按照第一轮勘测的方法继续处理。直到不可拆分出新的子序列为止。

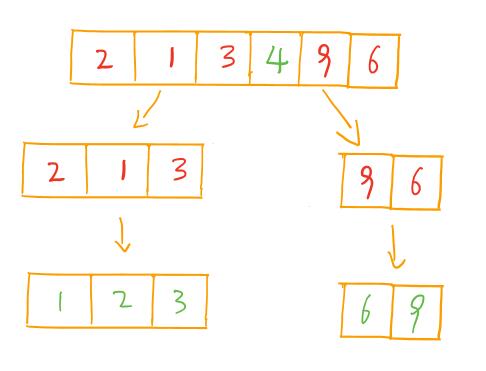
最终序列为

1 2 3 4 6 9

动态图如下：

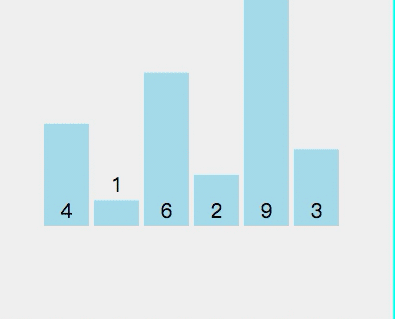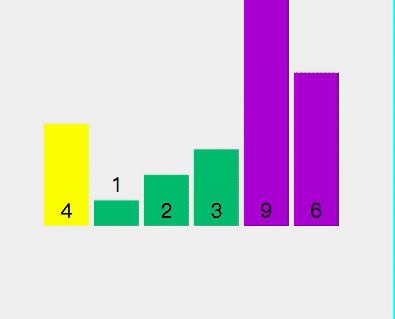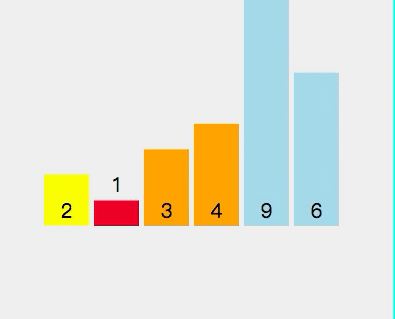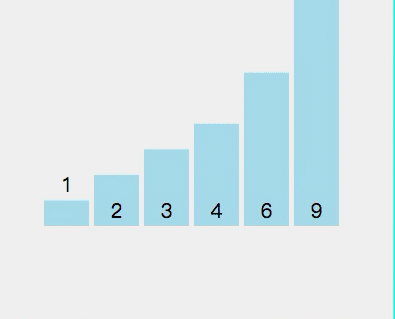
Java代码如下：

public class QuickSort {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(); //输入n个数
        int[] scores = new int[n];
        for (int i = 0; i < n; i++) //
            scores[i] = scanner.nextInt();

        //调用快速排序函数
        //quickSort(排序的数组，左边范围，右边范围 - 1)
        quickSort(scores, 0, scores.length - 1) ;

        for (int score : scores)
            System.out.print(score + " ");
    }
    public static void quickSort(int[] a, int left, int right){
        if(left >= right) {
            return;
        }
        int i = left;
        int j = right;
        int key = a[left]; //key存的是基准数

        while(i < j){
            //顺序很重要，要先从右往左边找
            while(a[j] >= key && i < j)
                j--;
            //再从左往右找
            while(a[i] <= key && i < j)
                i++;

            //交换两个数在数组中的位置
            if(i < j){  // 当哨兵i和哨兵j没有相遇时
                int t = a[i];
                a[i] = a[j];
                a[j] = t;
            }
        }

        //最终将基准数归位
        a[left] = a[i];
        a[i] = key;

        //递归处理
        quickSort(a, left, i-1); // 继续处理左边的，这里是一个递归的过程
        quickSort(a, i+1, right); // 继续处理右边的，这里是一个递归的过程
    }
}

输入数据

1 2	10 8 9 14 2 90 76 46 35 24 57

输出数据

1	2 8 9 14 24 35 46 57 76 90

快速排序之所以比较快，是因为相比冒泡排序，每次交换是跳跃式的。每次排序的时候设置一个基准点，将小于等于基准点的数全部放到基准点的左边，将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样只能在相邻的数之间进行交换，交换的距离就大得多了。因此总的比较和交换次数就少了，速度自然就提高了。当
然在坏的情况下，仍可能是相邻的两个数进行了交换。因此快速排序的差时间复杂度和冒泡排序是一样的，都是 O(N2)，它的平均时间复杂度为 O (NlogN)。

未完待续~~😘😘