数据结构-线性表（四）循环链表

数据结构

线性表（四）循环链表

思维导图

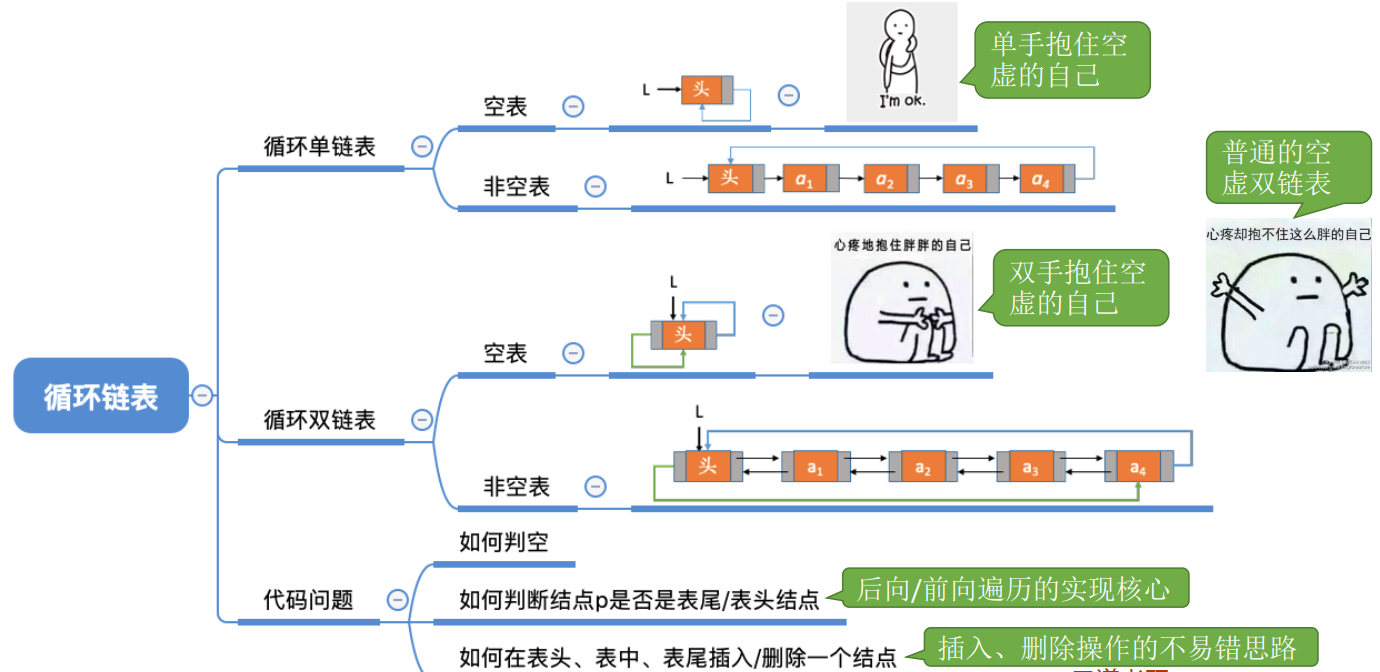
1 循环链表

（1）循环单链表

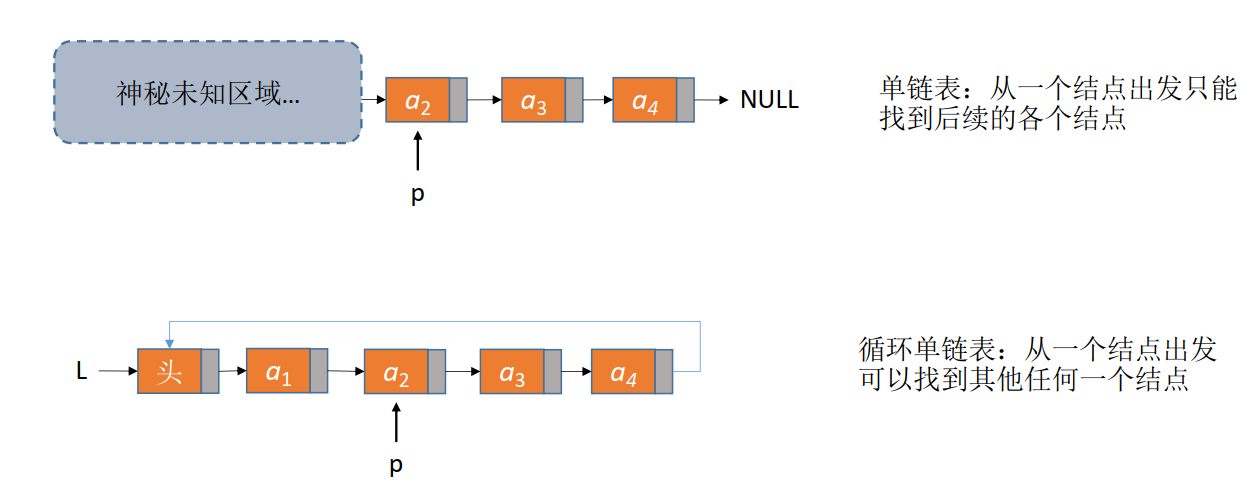
循环链表跟单链表的区在尾结点指针是指向链表的头结点。和单链表相比，循环链表的优点是从链尾到链头比较方便。当要处理的数据具有环

型结构特点时，采用循环链表实现代码会简洁很多。

代码

注意代码判空判满的实现

#include<iostream>
#include<stdlib.h>
#include<stdio.h>
using namespace std;

typedef struct LNode //定义单链表结点类型
{
    /* data */
    int data;           //数据域
    struct LNode *next; //指针域
} LNode, *LinkList;

/**
 * @description: 循环链表初始化
 */
bool InitList(LinkList &L)
{
    L = (LNode *)malloc(sizeof(LNode)); //分配内存空间
    if (L == NULL) //内存不足，分配失败
        return false;
    L->next = L; //头结点NEXT指向头结点
    //L = NULL; //空表
    return true;
}

/**
 * @description: 判断循环链表是否为空
 * @param {LinkList} L
 * @return {*}
 */
bool isEmpty(LinkList L) {
    return L->next == L;
}

/**
 * @description: 判断结点p是否为循环单链表的表尾结点
 * @param {LinkList} L
 * @param {LNode} *p
 * @return {*}
 */
bool isTail(LinkList L, LNode *p) {
    return p->next == L;
}
int main() {
    return 0;
}

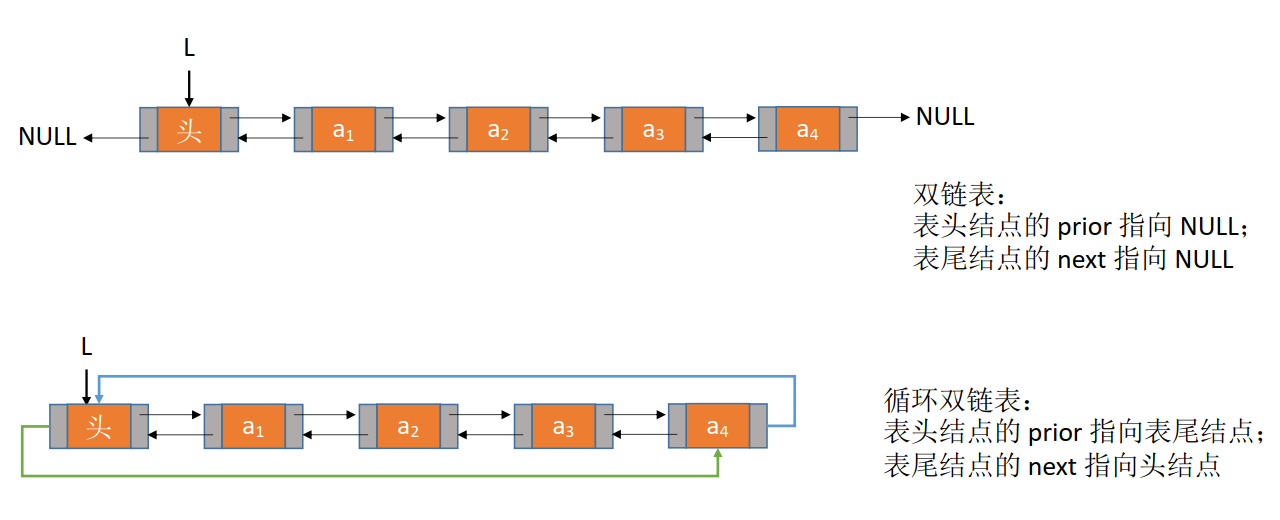
（2）循环双链表

#include<iostream>
#include<stdlib.h>
#include<stdio.h>
using namespace std;
typedef struct DoubleLinkedList
{
    int data;
    DoubleLinkedList *prior, *next;
} DNode, *DLinkList;

/**
 * 初始化
 */
bool InitDLinkList(DLinkList &L)
{
    L = (DNode *)malloc(sizeof(DNode));
    if (L == NULL)
        return false;
    L->prior = L;
    L->next = L;
    return true;
}

/**
 * @description: 判断循环链表是否为空
 * @param {DLinkList} L
 * @return {*}
 */
bool isEmpty(DLinkList L)
{
    return L->next == L && L->prior == L;
}

/**
 * @description: 判断结点p是否为循环单链表的表尾结点
 * @param {DLinkList} L
 * @param {DNode} *p
 * @return {*}
 */
bool isTail(DLinkList L, DNode *p)
{
    return p->next == L;
}
int main() {
    return 0;
}

（3）约瑟夫环问题

N个人坐成一个圆环（编号为1 - N），从第1个人开始报数✋，数到K的人出列，后面的人重新从1开始报数。问最后剩下的人的编号。

👉思路：

用一个不带头结点的循环链表来处理Josephu 问题：先构成一个有n个结点的单循环链表，然后由k结点起从1开始计数，计到m时，对应结点从链表中删除，然后再从被删除结点的下一个结点又从1开始计数，直到最后一个结点从链表中删除算法结束。

void Josephus ( int n, int m ) {
    Firster ( );                                //检验指针指向第一个结点
    for ( int i = 0; i < n-1; i++ ) {           //执行n-1次
        for ( int j = 0; j < m-1; j++ )  //循环m次使current指向被删除结点
            Next ( );
        cout << "出列的人是" << GetElem_L ( ) << endl;    //出列人员的数据
        ListDelete ( );                    //删去每一趟的第m结点
    }
}

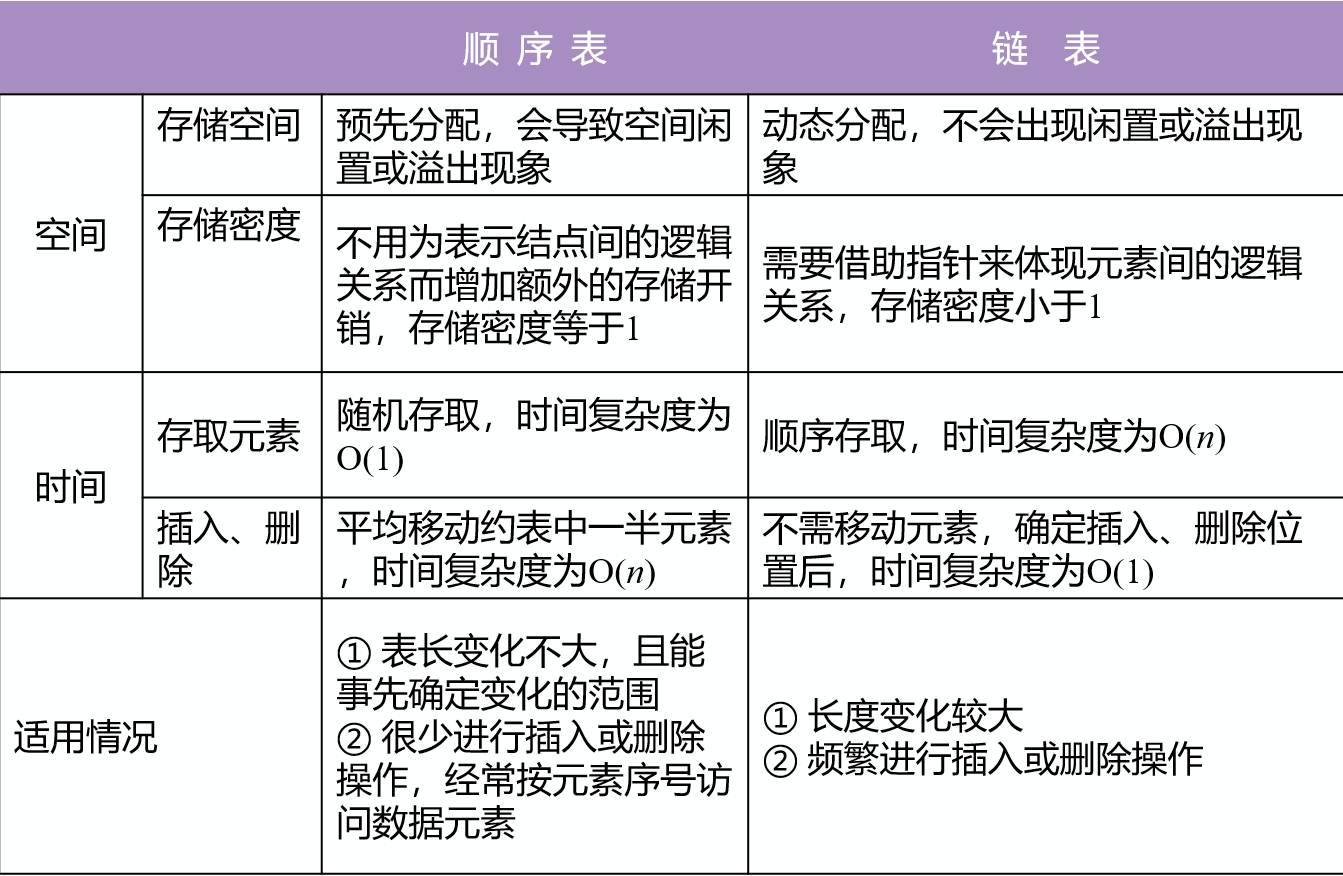
2 顺序表和链表比较

2.1 逻辑结构

都属于线性表，都是线性结构

2.2 存储结构

顺序表 ：顺序存储

• 优点：支持随机存取、存储密度高
• 缺点：大片连续空间分配不方便，改变容量不方便

链表：链式存储

• 优点：离散的小空间分配方便，改变容量方便
• 缺点：不可随机存取，存储密度低

2.3 基本操作

1、创

顺序表：

• 需要预分配大片连续空间。若分配空间过小，则之后不方便拓展容量；若分配空间过大，则浪费内存资源
• 静态分配：静态数组、容量不可改变
• 动态分配：动态数组（malloc、free） 容量可改变，但需要移动大量元素，时间代价高

链表：

只需分配一个头结点（也可以不要头结点，只声明一个头指针），之后方便拓展

2、销

顺序表：

修改 Length = 0

静态分配：静态数组、系统自动回收空间

动态分配：动态数组（malloc、free）需要手动 free

链表：

依次删除各个结点（free）

3、增、删

顺序表：

1. 插入/删除元素要将后续元素都后移/前移
2. 时间复杂度 O(n)，时间开销主要来自移动元素
3. 若数据元素很大，则移动的时间代价很高

链表：

1. 插入/删除元素只需修改指针即可
2. 时间复杂度 O(n)，时间开销主要来自查找目标元素
3. 查找元素的时间代价更低

4、查

顺序表：

1. 按位查找：O(1)
2. 按值查找：O(n)
   若表内元素有序，可在O(log2n) 时间内找到

链表：

1. 按位查找：O(n)
2. 按值查找：O(n)

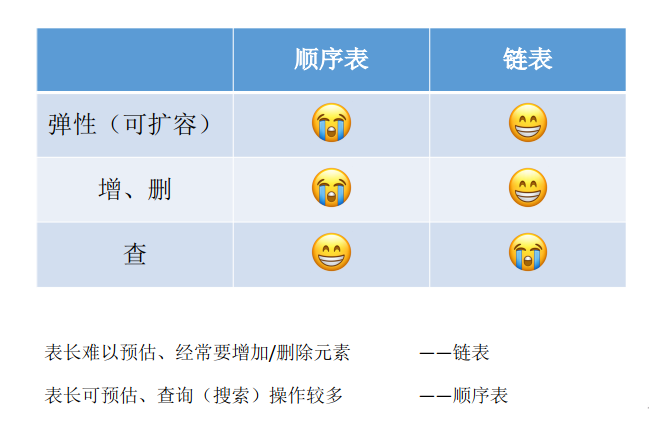
2.4 选择