数据结构

栈和队列（三）栈和队列的应用

1 栈在括号匹配应用

1.1 算法流程图

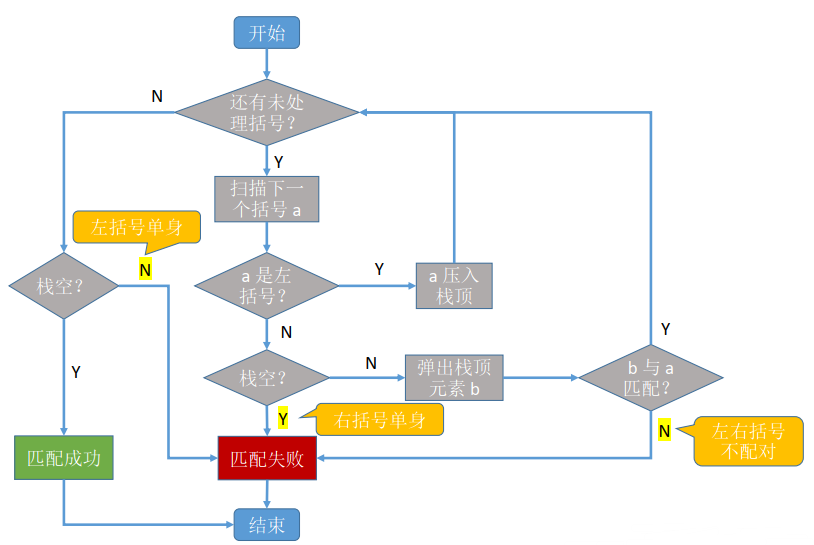
1.2 代码实现

（1）判断括号是否匹配

#include<iostream>
#include <string>
#include<stack>
using namespace std;

bool bracketCheck(string str) {
    stack<char> s;
    for(int i = 0; i < str.length(); i++) {
        if (str[i] == '(' || str[i] == '[' || str[i] == '{'){  //左括号入栈
            s.push(str[i]);
        } else if(s.empty()) { //栈空失败
            return false;
        } else {
            char t;
            t = s.top(); //匹配右括号
            if (str[i] == ')' && t == '(') {
                s.pop();    
            }
            else if (str[i] == ']' && t == '[')
            {
                s.pop();
            }
            else if (str[i] == '}' && t == '{')
            {
                s.pop();
            }else
                return false;
        }
    }
    return s.empty(); //匹配结束，栈空匹配成功
}

int main() {
    
    string str;
    cin >> str;
    cout << bracketCheck(str) << endl;
    return 0;
}

1 2	([]{}(())) 1

（2）n对括号可以有多少种匹配排列方式

算法链接 https://blog.csdn.net/u014529413/article/details/39119273

#include<iostream>
#include <string>
using namespace std;

int n, num = 0;
void dfs(int l, int r, int n, string s, int &num)
{
    if (r == n)
    {
        cout << s << endl;
        num++;
        return;
    }
    if (r == l)
    {
        s.append("(");
        l++;
        dfs(l, r, n, s, num);
    }
    else //r<l
    {
        if (l == n)
        {
            s.append(")");
            r++;
            dfs(l, r, n, s, num);
        }
        else
        {
            s.append("(");
            l++;
            dfs(l, r, n, s, num);
            s = s.substr(0, s.length() - 1);
            l--;
            s.append(")");
            r++;
            dfs(l, r, n, s, num);
        }
    }
}
int main()
{
    cin >> n;
    string s;
    dfs(0, 0, n, s, num);
    cout << num;
    return 0;
}

3
((()))
(()())
(())()
()(())
()()()
5

2 栈在表达式求值应用

思维导图

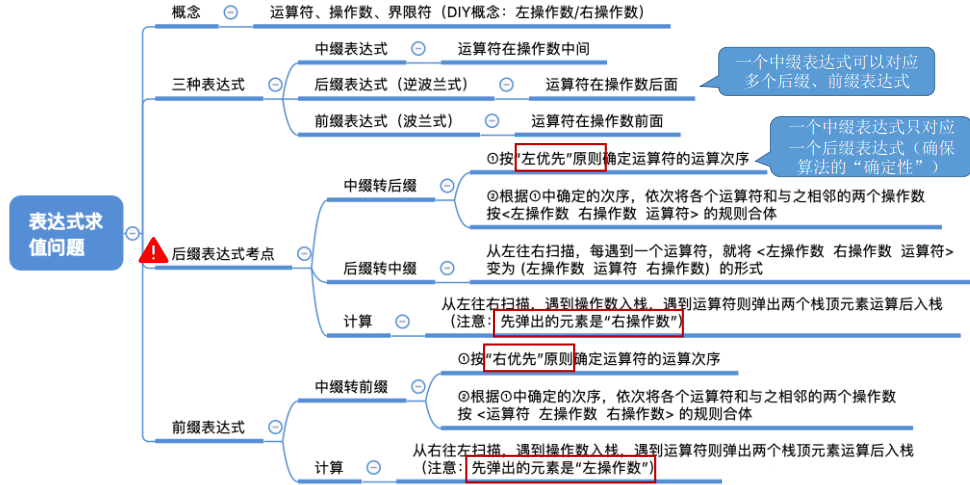
2.1 中缀表达式

中缀表达式是一个通用的算术或逻辑公式表示方法， 操作符是以中缀形式处于操作数的中间，中缀表达式是人们常用的算术表示方法，

比如（499 + 1）* 2 + 314

2.2 前缀表达式

前缀表达式是一种没有括号的算术表达式，与中缀表达式不同的是，其将运算符写在前面，操作数写在后面。也被叫做波兰表达式,

比如（499 + 1）* 2 + 314 的前缀表达式为 + * + 499 1 2 314

求值方法：

（1）从右至左扫描表达式，遇到数字时，将数字压入栈；

（2）遇到运算符时，弹出栈顶的两个数；

（3）用运算符对它们做相应的计算（栈顶元素和次顶元素），并将结果入栈；

（4）重复上述过程直到表达式最左端，最后运算得出的值即为表达式的结果；

举栗子🌰🌰（499 + 1）* 2 + 314 对应的前缀表达式就是 + * + 499 1 2 314, 针对前缀表达式求值步骤如下:

从右至左扫描，将314、2、1、499压入堆栈

遇到+运算符，因此弹出499和1（499为栈顶元素，1为次顶元素），计算499 + 1的值，得500，再将500入栈

接下来是 * 运算符，因此弹出500和2（500为栈顶元素，2为次顶元素），计算500 * 2的值，得1000，再将1000入栈

最后是+运算符，计算出1000 + 314的值，即1314💝💝，由此得出最终结果

2.3 后缀表达式

逆波兰式（或逆波兰记法），也叫后缀表达式，其将运算符写在操作数之后，后缀表达式源自于前缀表达式，为了区分前缀和后缀表示，通常将后缀表示称为逆波兰表示。

比如：（499 + 1）x 2 + 314 的后缀表达试为 499 1 + 2 x 314 +

求值方法：

（1）从左至右扫描表达式，遇到数字时，将数字压入堆栈；

（2）遇到运算符时，弹出栈顶的两个数；

（3）用运算符对它们做相应的计算（次顶元素和栈顶元素），并将结果入栈；

（4）重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果。

举栗子🌰🌰（499 + 1）* 2 + 314 对应的后缀表达式就是 499 1 + 2 * 314 +, 针对前缀表达式求值步骤如下:

从左至右扫描，将499和1压入堆栈；

遇到+运算符，因此弹出499和1（1为栈顶元素，499为次顶元素），计算出499+1的值，得500，再将500入栈；

将2入栈；

接下来是 * 运算符，因此弹出500和2，计算出500 * 2，得1000，再将1000入栈；

将314入栈；

最后是+运算符，计算出1000+314的值，即1314💗💗，由此得出最终结果

2.4 中缀转后缀表达式

转换算法步骤📋👇

初始化两个栈：运算符栈s1和储存中间结果的栈s2；

从左至右扫描中缀表达式；

遇到操作数时，将其压s2栈；

遇到运算符时，比较其与s1栈顶运算符的优先级：

4.1.如果s1为空，或栈顶运算符为左括号“ ( ”，则直接将此运算符入栈；

4.2.否则，若优先级比栈顶运算符的高，也将运算符压入s1；

4.3.否则，将s1栈顶的运算符弹出并压入到s2中，再次转到(4.1)与s1中新的栈顶运算符相比较；

遇到括号时：
(1) 如果是左括号“ ( ”，则直接压入s1
(2) 如果是右括号“ ) ”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃

重复步骤2至5，直到表达式的最右边

将s1中剩余的运算符依次弹出并压入s2

依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

注：中缀表达式转为前缀表达式是从又往左扫描中缀表达式，核心算法思想相同😄😄

实例分析

将中缀表达式1+((2+3)*4)-5转换为后缀表达式。

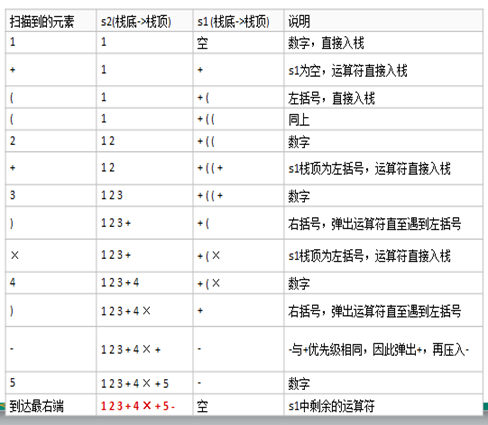
按照步骤最终结果为：1 2 3 + 4 * + 5 -

2.5 中缀转前缀表达式

中缀表达式转为前缀表达式是从又往左扫描中缀表达式，核心算法思想与中缀转后缀表达式相同

2.6 总结

用栈实现中缀表达式转后缀表达式：

初始化一个栈，用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素，直到末尾。可能遇到三种情况：

① 遇到操作数。直接加入后缀表达式。

② 遇到界限符。遇到“(”直接入栈；遇到“)”则依次弹出栈内运算符并加入后缀表达式，直到弹出“(”为止。注意：“(”不加入后缀表达式。

③ 遇到运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符，并加入后缀表达式，若碰到“(” 或栈空则停止。之后再把当前运算符入栈。按上述方法处理完所有字符后，将栈中剩余运算符依次弹出，并加入后缀表达式。

用栈实现后缀表达式的计算：

①从左往右扫描下一个元素，直到处理完所有元素

②若扫描到操作数则压入栈，并回到①；否则执行③

③若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到①

用栈实现中缀表达式的计算：

①初始化两个栈，操作数栈和运算符栈

②若扫描到操作数，压入操作数栈

③若扫描到运算符或界限符，则按照“中缀转后缀”相同的逻辑压入运算符栈（期间也会弹出运算符，每当弹出一个运算符时，就需要再弹出两个操作数栈的栈顶元素并执行相应运算，运算结果再压回操作数栈）

3 栈在递归中的应用

函数调用的特点：最后被调用的函数最先执行结束（LIFO）

函数调用时，需要用一个栈存储：
① 调用返回地址
② 实参
③ 局部变量

递归调用时，函数调用栈可称为“递归工作栈”
每进入一层递归，就将递归调用所需信息压入栈顶
每退出一层递归，就从栈顶弹出相应信息

缺点：

效率低；

太多层递归可能会导致栈溢出；

可能包含很多重复计算

4 队列应用

树、图的广度优先遍历和操作系统中的应用（进程调度算法、磁盘算法、页面缺失算法）