数据结构-串和数组(三)KMP算法
1、算法思想
由D.E.Knuth,J.H.Morris和V.R.Pratt提出,因此称为 KMP算法;
根据模式串T,求出 next 数组。利用next数组进行匹配(主串指针不回溯)next数组只和短短的模式串有关,和长长的主串无关
2、复杂度分析
时间复杂度:
KMP算法, 最坏时间复杂度 O(m+n)
其中,求 next 数组时间复杂度 O(m)
模式匹配过程最坏时间复杂度 O(n)
3、 next数组求解
next数组的作用:当模式串的第 j 个字符失配时,从模式串的第 next[j] 的继续往后匹配
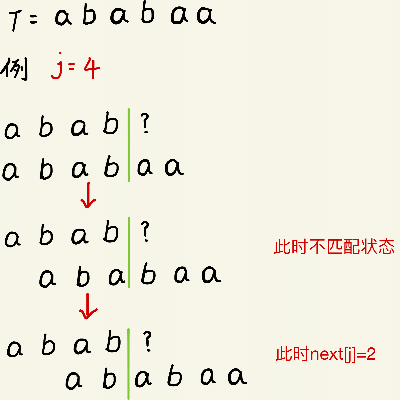
1、手动移位模拟法
next[1] 都⽆脑写 0
next[2] 都⽆脑写 1
其他 next: 在不匹配的位置前,划⼀根美丽的分界线;模式串⼀步⼀步往后退,直到分界线之前“能对上”,或模式串完全跨过分界线为⽌。
此时 j 指向哪⼉, next数组值就是多少;
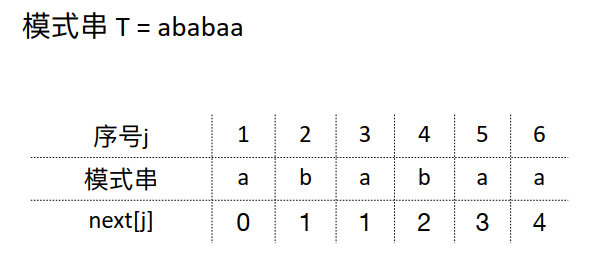
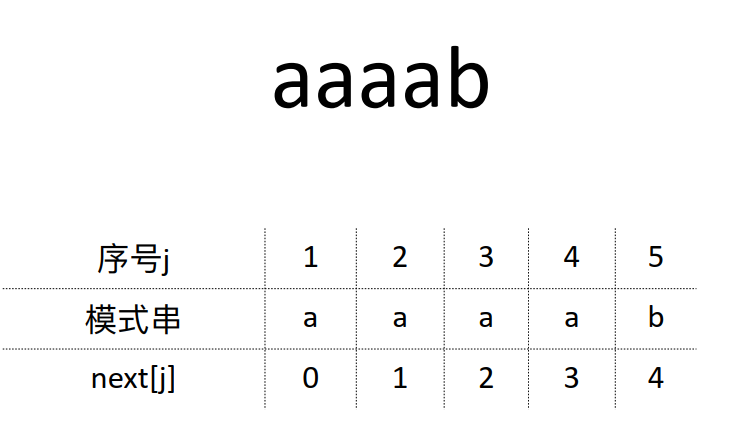
2、前后缀计算法
next[j] = 字符串的前缀和后缀的最长相等前后缀长度 + 1
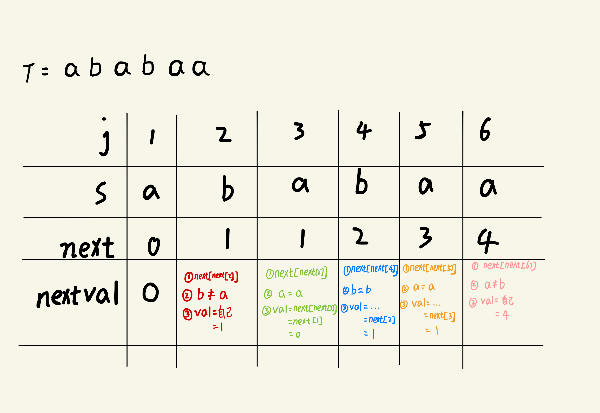
4、 KMP算法优化
先得出next数组,然后从头开始遍历
1、先找对应的next[next[j]]
2、判断该字符是否相等
3、相等,则nextval[j] = next[next[j]],即等于找到的next数组值
4、不相等,则nextval[j] = next[j],即等于自身next数组值