数据结构-树和二叉树（一）基本概念

1 树的基本概念

思维导图

1.1 定义

树是n（n≥0）个结点的有限集合， n = 0时，称为空树，这是一种特殊情况。

在任意一棵非空树中应满足：

1、有且仅有一个特定的称为根的结点。

2、当n > 1时，其余结点可分为m（m > 0）个互不相交的有限集合T1, T2,…, Tm，其中每个集合本身又是一棵树，并且称为根结点的子树。

树的定义是递归的，即在树的定义中又用到了其自身，树是一种递归的数据结构。

树作为一种逻辑结构，同时也是一种分层结构，具有以下两个特点：

🌲除了根节点外，任何一个结点都有且仅有一个前驱

🌳中所有结点可以有零个或多个后继

非空树的特性：
🌲有且仅有一个根节点
🌳没有后继的结点称为“叶子结点”（或终端结点）
🌴有后继的结点称为“分支结点”（或非终端结点）
🌱除了根节点外，任何一个结点都有且仅有一个前驱
🌵每个结点可以有0个或多个后继。

1.2 基本术语

属性

结点的度（Degree）：结点的子树个数；

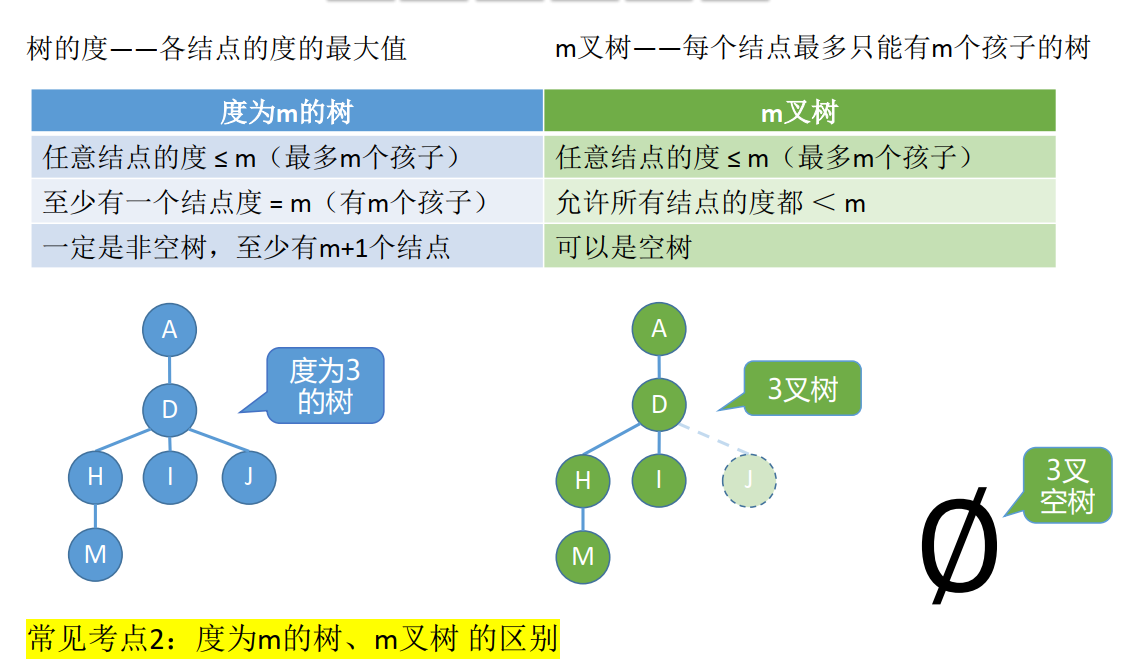
树的度：树的所有结点中最大的度数；

叶子结点（Leaf）：度为0的结点；也叫终端结点。

父结点（Parent）：有子树的结点是其子树的根节点的父结点；

子结点/孩子结点（Child）：若A结点是B结点的父结点，则称B结点是A结点的子结点；

兄弟结点（Sibling）：具有同一个父结点的各结点彼此是兄弟结点；

路径和路径长度：从结点$n_1$到$n_k$的路径为一个结点序列$n_1，n_2，…，n_k$。$n_i$是$n_i+1$的父结点。路径所包含边的个数为路径的长度；

祖先结点（Ancestor）：沿树根到某一结点路径上的所有结点都是这个结点的祖先结点；

子孙结点（Descendant）：某一结点的子树中的所有结点是这个结点的子孙；

结点的层次（Level）：规定根结点在1层，其他任一结点的层数是其父结点的层数加1；

树的深度（Depth）：树中所有结点中的最大层次是这棵树的深度；

有序树——逻辑上看，树中结点的各子树从左至右是有次序的，不能互换

无序树——逻辑上看，树中结点的各子树从左至右是无次序的，可以互换

森林：森林是m（m≥0）棵互不相交的树的集合

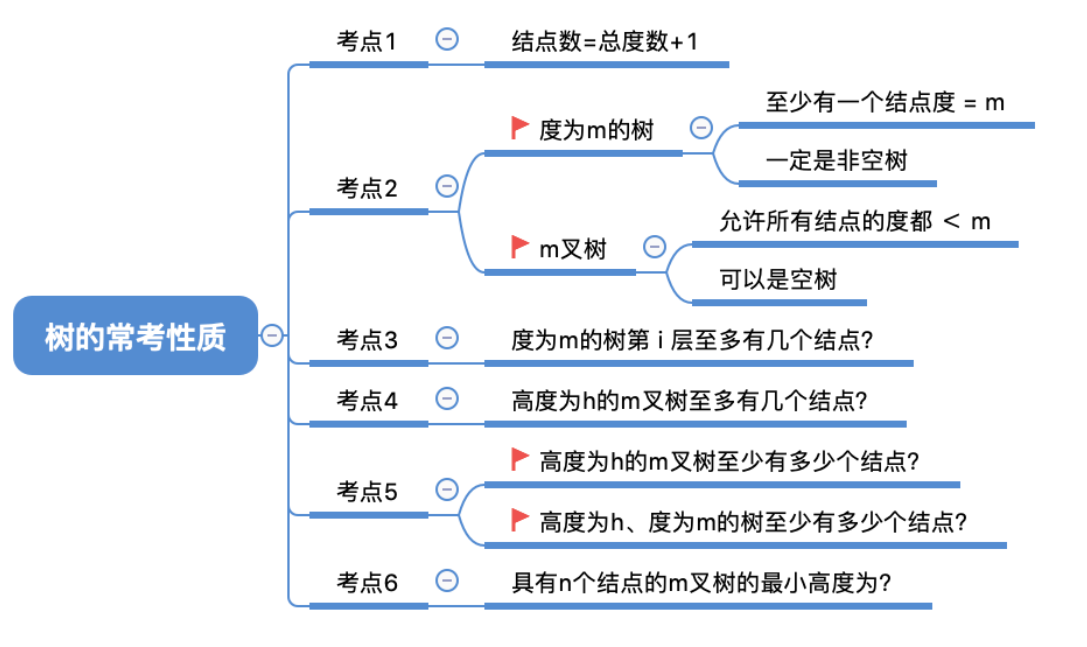
1.3 树的性质

树中的结点数 = 总度数 + 1

度为 m 的树第 i 层至多有$m^{i-1}$ 个结点（i ≥ 1）

高度为 h 的 m 叉树至多有 $(m^{h- 1}) / (m - 1)$个结点。

高度为 h 的 m 叉树至少有 h 个结点；高度为h、度为m的树至少有 h + m - 1 个结点。

具有 n 个结点的 m 叉树的最小高度为 $[log_m(n (m - 1) + 1)]$

度为m的树、m叉树的区别

2 二叉树🌱的基本概念

思维导图

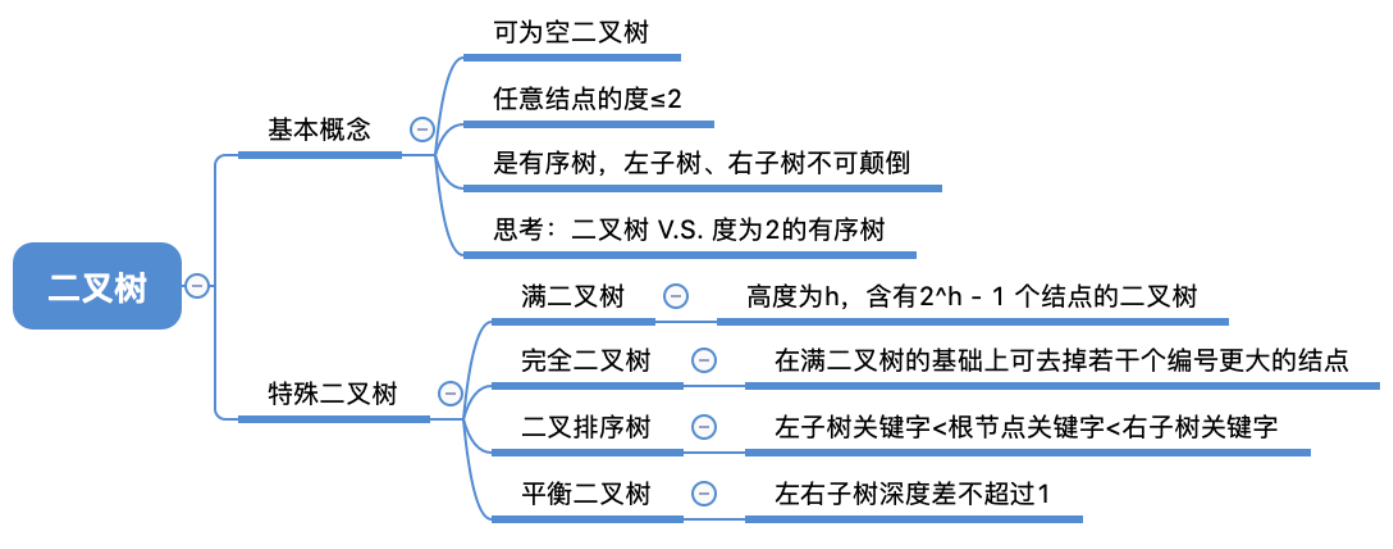
2.1 定义

二叉树是n（n≥0）个结点的有限集合：

① 或者为空二叉树，即n = 0。

② 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。

特点：

① 每个结点至多只有两棵子树

② 左右子树不能颠倒（二叉树是有序树）

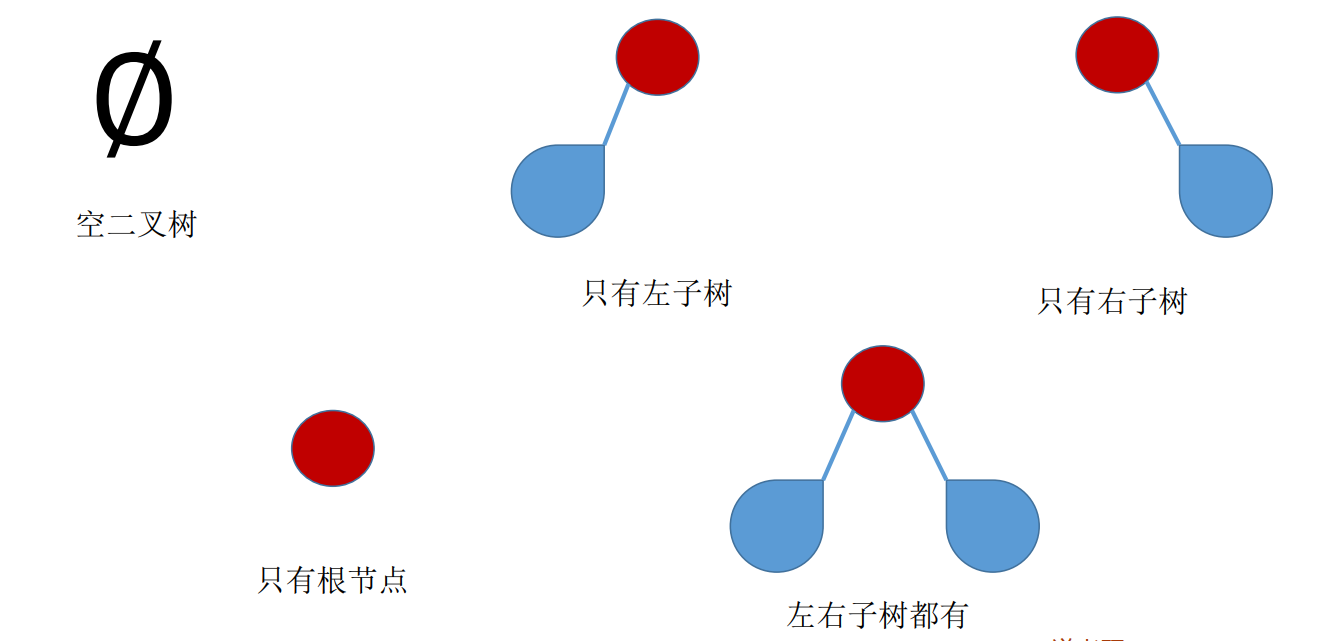
二叉树的五种形态

特殊的二叉树

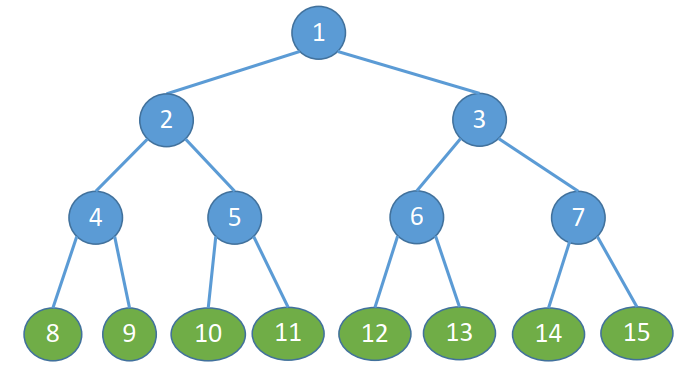
1、满二叉树。 一棵高度为h，且含有$2^h - 1$个结点的二叉树

特点：
① 只有最后一层有叶子结点

② 不存在度为 1 的结点

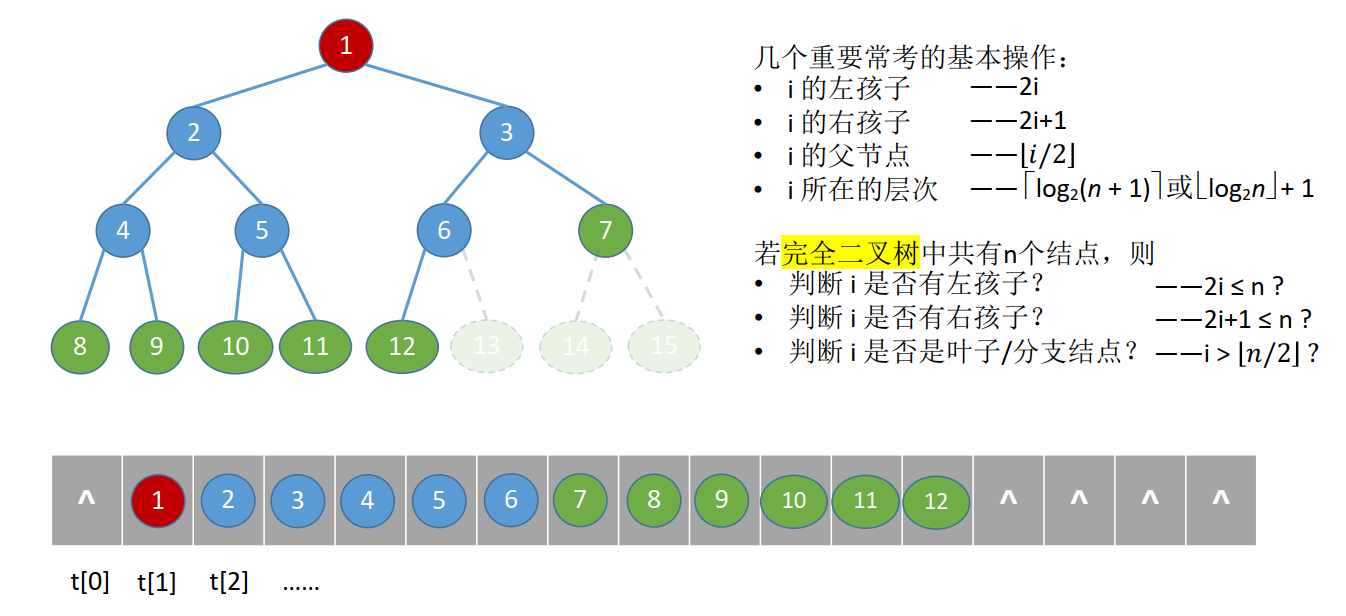
③ 按层序从 1 开始编号，结点 i 的左孩子为 2i，右孩子为 2i + 1；结点 i 的父节点为 i / 2 （如果有的话）

2、完全二叉树。当且仅当其每个结点都与高度为h的满二叉树中编号为1～n的结点一一对应时，称为完全二叉树。

特点：
① 只有最后两层可能有叶子结点

② 最多只有一个度为1的结点

③ 按层序从 1 开始编号，结点 i 的左孩子为 2i，右孩子为 2i + 1；结点 i 的父节点为 i / 2 （如果有的话）

④ i≤ 𝑛/2 为分支结点， i> 𝑛/2 为叶子结点

注：如果某结点只有一个孩子，那么一定是左孩子

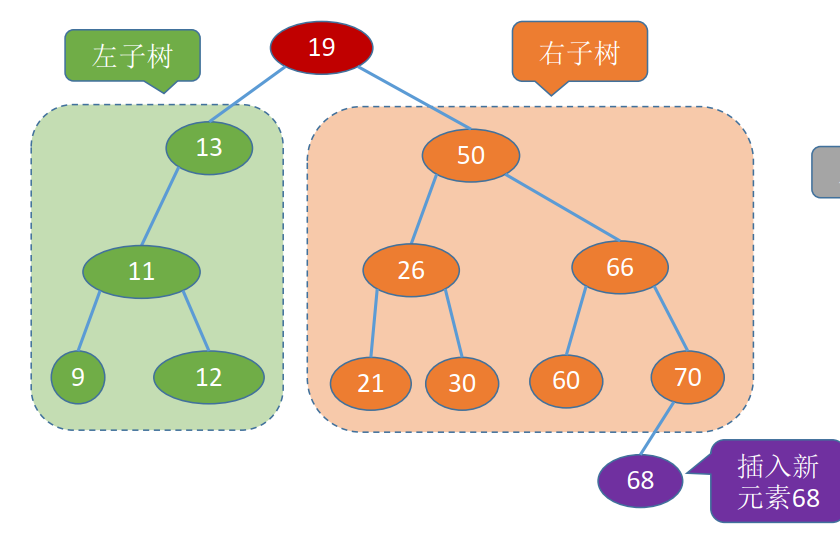
3、二叉排序树。一棵二叉树或者是空二叉树，或者是具有如下性质的二叉树：

① 左子树上所有结点的关键字均小于根结点的关键字；

② 右子树上所有结点的关键字均大于根结点的关键字。

③ 左子树和右子树又各是一棵二叉排序树。

二叉排序树可用于元素的排序、搜索

4、平衡二叉树。树上任一结点的左子树和右子树的深度之差不超过1。平衡二叉树能有更高的搜索效率。

2.2 性质

1、设非空二叉树中度为0、 1和2的结点个数分别为$n_0$、 $n_1$和 $n_2$，则 $n_0$ = $n_2$ + 1（叶子结点比二分支结点多一个）

2、二叉树第 i 层至多有$2^i - 1$ 个结点（i≥1）；

m叉树第 i 层至多有$m^i - 1$ 个结点（i≥1）

3、高度为 h 的二叉树至多有 $2^ℎ - 1$个结点（满二叉树）；高度为h的m叉树至多有($m^{h - 1}$) / (m - 1)个结点。

4、具有 n 个（n > 0）结点的完全二叉树的高度 h 为$[log_2(n + 1)]$ 或 $[log_2n]+1 $

高为 h - 1 的满二叉树共有 $2^ℎ - 1$个结点

高为 h 的完全二叉树至少$2^{h - 1}$个结点，至多 $2^ℎ - 1$ 个结点

5、对于完全二叉树，可以由的结点数 n 推出度为0、 1 和 2 的结点个数为$n_0$、 $n_1$和$n_2$

完全二叉树最多只有一个度为 1 的结点，即 $n_1$ = 0 或 1

$n_0$ = $n_2$+ 1 —–> n0 + n2 一定是奇数

若完全二叉树有 2k 个（偶数）个结点，则必有 $n_1$ = 1， $n_0$ = k， $n_2$ = k - 1

若完全二叉树有 2k - 1 个（奇数）个结点，则必有 $n_1$=0， $n_0$ = k， $n_2$ = k - 1

2.3 存储结构

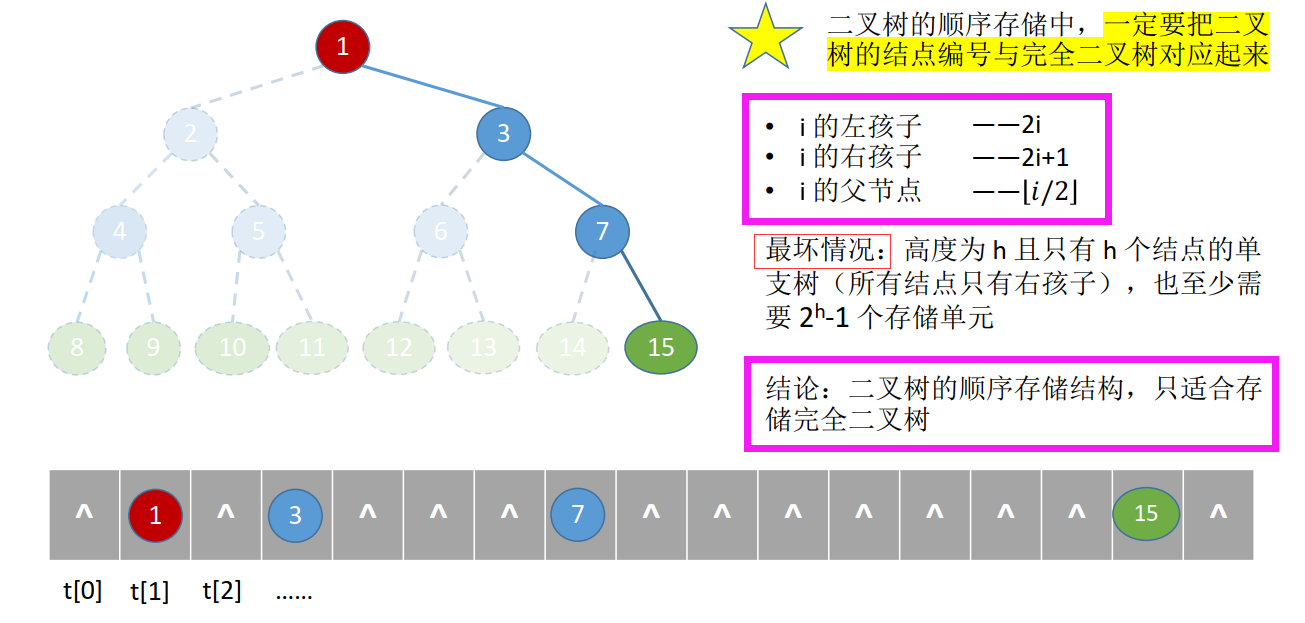
1、顺序存储结构

实现：按满二叉树的结点层次编号，依次存放二叉树中的数据元素。

特点：

结点间关系蕴含在其存储位置中，浪费空间，适于存满二叉树和完全二叉树

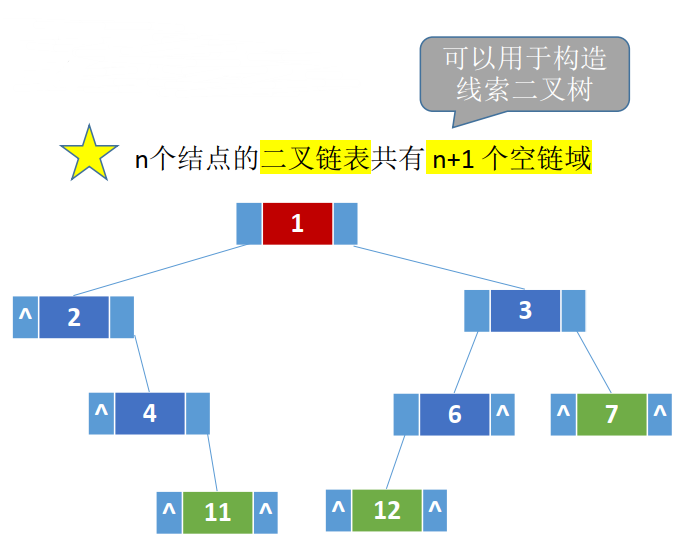
2、链式存储结构

n个结点的二叉链表共有 n+1 个空链域

代码实现

#include <iostream>
#include <string>
using namespace std;
typedef struct BiTNode {
    int value; //数据域
    struct BiTNode *lChild, *rChild; //左、右孩子指针
}BiTNode, *BiTree;

/**
 * 创建二叉树
 * @param root
 * @return
 */
bool CreateBiTNode(BiTree &root) {
    root = (BiTNode *)malloc(sizeof(BiTNode));
    int e;
    cin >> e;
    if (e == -1) {
        root = NULL;
    } else {
        root->value = e;
        root->lChild = nullptr;
        root->rChild = nullptr;
        cout << "请输入" << e << "左结点值（-1代表无子结点）：" <<  endl;
        CreateBiTNode(root->lChild);
        cout << "请输入" << e << "右结点值（-1代表无子结点）：" <<  endl;
        CreateBiTNode(root->rChild);
    }

}

//先序遍历二叉树
void TraverseBiTree(BiTree T) {
    if (T == NULL) {
        return;
    }
    cout << T->value << "->" << endl;
    TraverseBiTree(T->lChild);
    TraverseBiTree(T->rChild);
}

int main() {
    BiTree root;
    cout << "请输入结点值（-1代表无子结点）：" <<  endl;
    CreateBiTNode(root);
    cout << "先序遍历二叉树" <<  endl;
    TraverseBiTree(root);
    return 0;
}

请输入结点值（-1代表无子结点）：
1
请输入1左结点值（-1代表无子结点）：
2
请输入2左结点值（-1代表无子结点）：
-1
请输入2右结点值（-1代表无子结点）：
-1
请输入1右结点值（-1代表无子结点）：
3
请输入3左结点值（-1代表无子结点）：
4
请输入4左结点值（-1代表无子结点）：
-1
请输入4右结点值（-1代表无子结点）：
-1
请输入3右结点值（-1代表无子结点）：
-1
先序遍历二叉树
1->
2->
3->
4->

Process finished with exit code 0