数据结构-树和二叉树（二）二叉树的遍历

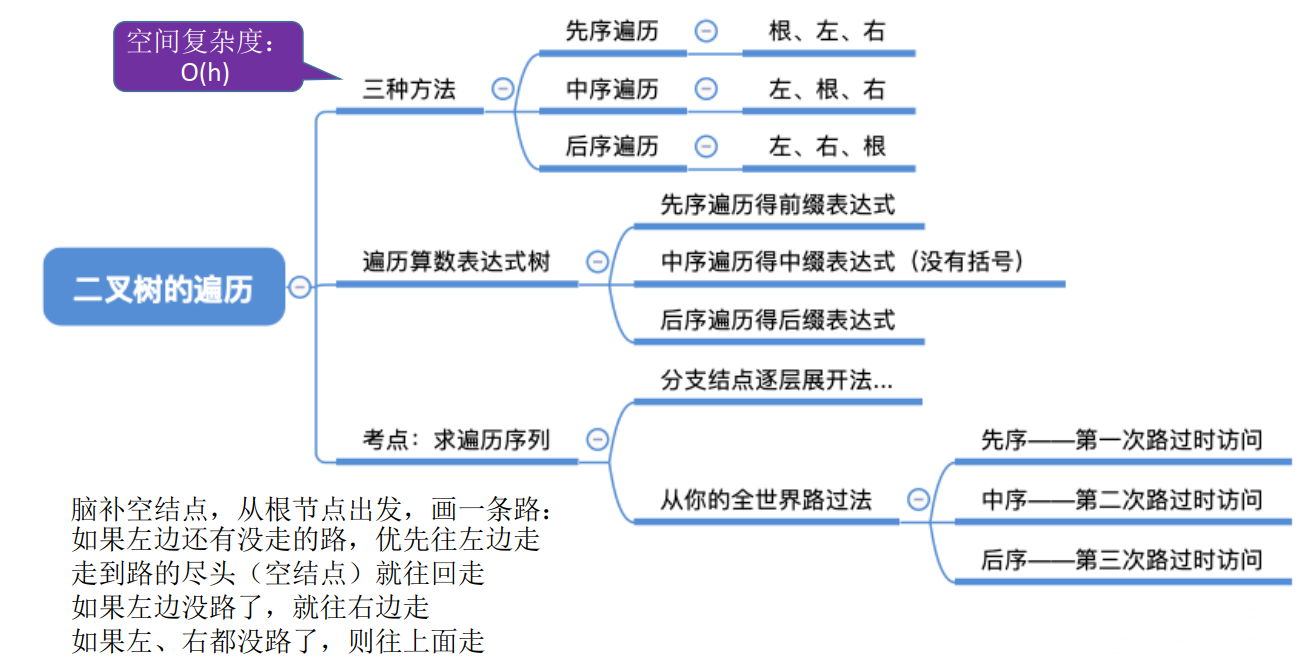
1 先序遍历

DLR—先序遍历，即先根再左再右

先序遍历（PreOrder）的操作过程如下：

1. 若二叉树为空，则什么也不做；

2. 若二叉树非空：

   ①访问根结点；

   ②先序遍历左子树；

   ③先序遍历右子树。

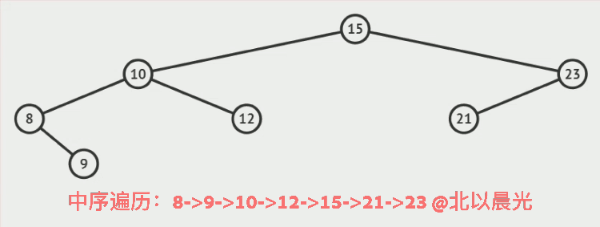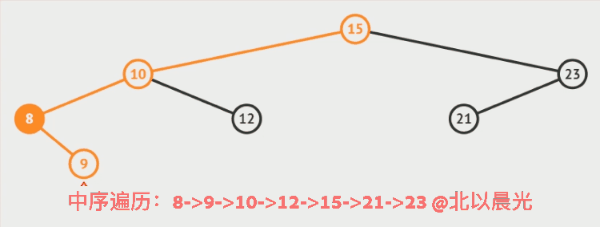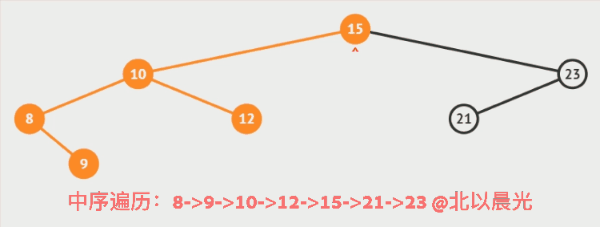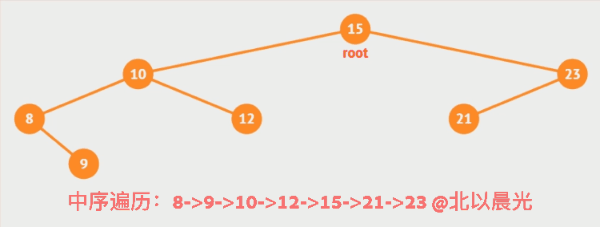
2 中序遍历

LDR—中序遍历，即先左再根再右

中序遍历（InOrder）的操作过程如下：

1. 若二叉树为空，则什么也不做；

2. 若二叉树非空：

   ①中序遍历左子树；

   ②访问根结点；

   ③中序遍历右子树。

3 后序遍历

LRD—后序遍历，即先左再右再根

后序遍历（PostOrder）的操作过程如下：

1. 若二叉树为空，则什么也不做；

2. 若二叉树非空：

   ①后序遍历左子树；

   ②后序遍历右子树；

   ③访问根结点。

4 层次遍历

算法思想：

①初始化一个辅助队列

②根结点入队

③若队列非空，则队头结点出队，访问该结点，并将其左、右孩子插入队尾（如果有的话）

④重复③直至队列为空

5 代码实现

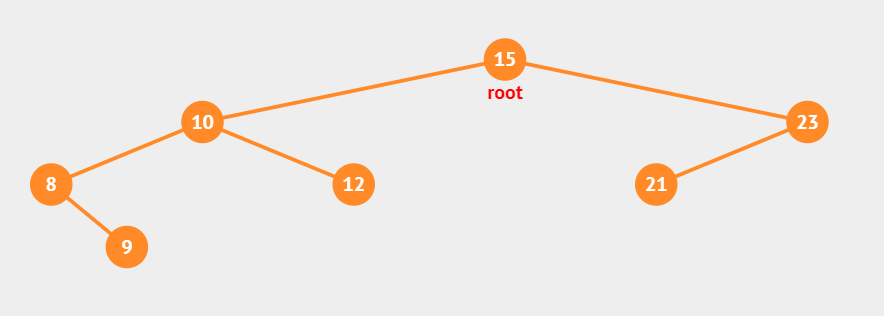
实现对如图二叉树创建和遍历

#include <iostream>
#include <string>
#include <queue>
using namespace std;
typedef struct BiTNode {
    int value; //数据域
    struct BiTNode *lChild, *rChild; //左、右孩子指针
}BiTNode, *BiTree;

/**
 * 创建二叉树
 * @param root
 * @return
 */
bool CreateBiTNode(BiTree &root) {
    //创造新结点
    auto *node1 = (BiTNode *)malloc(sizeof(BiTNode));
    auto *node2 = (BiTNode *)malloc(sizeof(BiTNode));
    auto *node3 = (BiTNode *)malloc(sizeof(BiTNode));
    auto *node4 = (BiTNode *)malloc(sizeof(BiTNode));
    auto *node5 = (BiTNode *)malloc(sizeof(BiTNode));
    auto *node6 = (BiTNode *)malloc(sizeof(BiTNode));
    //为结点赋值
    root->value = 15;
    node1->value = 10;
    node2->value = 23;
    node3->value = 8;
    node4->value = 12;
    node5->value = 21;
    node6->value = 9;
    //分层赋子节点
    root->lChild = node1;
    root->rChild = node2;
    //
    node1->lChild = node3;
    node1->rChild = node4;
    node2->lChild = node5;
    node2->rChild = nullptr;
    //
    node3->lChild = nullptr;
    node3->rChild = node6;
    node4->lChild = nullptr;
    node4->rChild = nullptr;
    node5->rChild = nullptr;
    node5->lChild = nullptr;
    //
    node6->lChild = nullptr;
    node6->rChild = nullptr;
}


/**
 * 先序遍历--先根再左再右
 * @param root
 */
void PreOrderTraversal(BiTree root) {
    if (root == NULL) {
        return;
    }
    cout << root->value << "->";
    PreOrderTraversal(root->lChild); //先序遍历左子树
    PreOrderTraversal(root->rChild); //先序遍历右子树
}

/**
 * 中序遍历--先左再根再右
 * @param root
 */
void InOrderTraversal(BiTree root) {
    if (root == NULL) {
        return;
    }
    InOrderTraversal(root->lChild); //中序遍历左子树
    cout << root->value << "->";
    InOrderTraversal(root->rChild); //中序遍历右子树
}

/**
 * 后序遍历--先左再右再根
 * @param root
 */
void PostOrderTraversal(BiTree root) {
    if (root == nullptr) {
        return;
    }
    PostOrderTraversal(root->lChild); //后序遍历左子树
    PostOrderTraversal(root->rChild); //h序遍历右子树
    cout << root->value << "->";
}

/**
 * 层次遍历
 * @param root
 */
void LevelOrderTraversal(BiTree root) {
    queue<BiTNode *> tree; //声明队列
    tree.push(root); //根节点入队
    while (!tree.empty()) { //当队列不为空
        BiTNode *p = tree.front();  //队头结点出队
        tree.pop();
        cout << p->value << "->";  //打印队头结点数据
        if (p->lChild != nullptr) { //左子树不为空，左子树根节点入队
            tree.push(p->lChild);
        }
        if (p->rChild != nullptr) { //左子树不为空，左子树根节点入队
            tree.push(p->rChild);
        }
    }

}
int main() {
    BiTree root;
    root = (BiTNode *)malloc(sizeof(BiTNode));
    cout << "初始化创建二叉树" <<  endl;
    CreateBiTNode(root);
    cout << "先序遍历二叉树--先左再根再右" <<  endl;
    PreOrderTraversal(root);
    printf("\n");
    cout << "中序遍历二叉树--先左再根再右" <<  endl;
    InOrderTraversal(root);
    printf("\n");
    cout << "后序遍历二叉树--先左再右再根" <<  endl;
    PostOrderTraversal(root);
    printf("\n");
    cout << "层次遍历二叉树--按层次遍历" <<  endl;
    LevelOrderTraversal(root);
    return 0;
}

初始化创建二叉树
先序遍历二叉树--先左再根再右
15->10->8->9->12->23->21->
中序遍历二叉树--先左再根再右
8->9->10->12->15->21->23->
后序遍历二叉树--先左再右再根
9->8->12->10->21->23->15->
层次遍历二叉树--按层次遍历
15->10->23->8->12->21->9->
Process finished with exit code 0

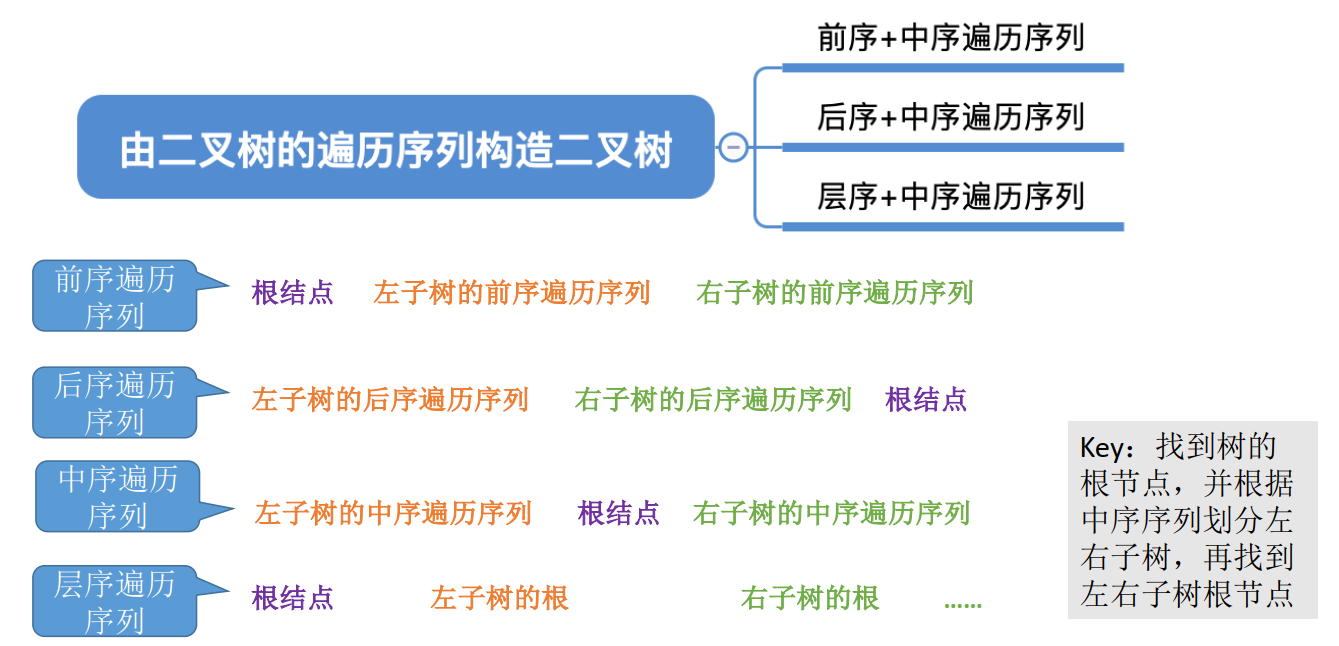
6 由遍历序列构造二叉树