0%

数据结构-树和二叉树（三）二叉树线索化

发表于 更新于 分类于
本文字数： 7.2k 阅读时长 ≈ 7 分钟

数据结构-树和二叉树（三）二叉树线索化

思维导图

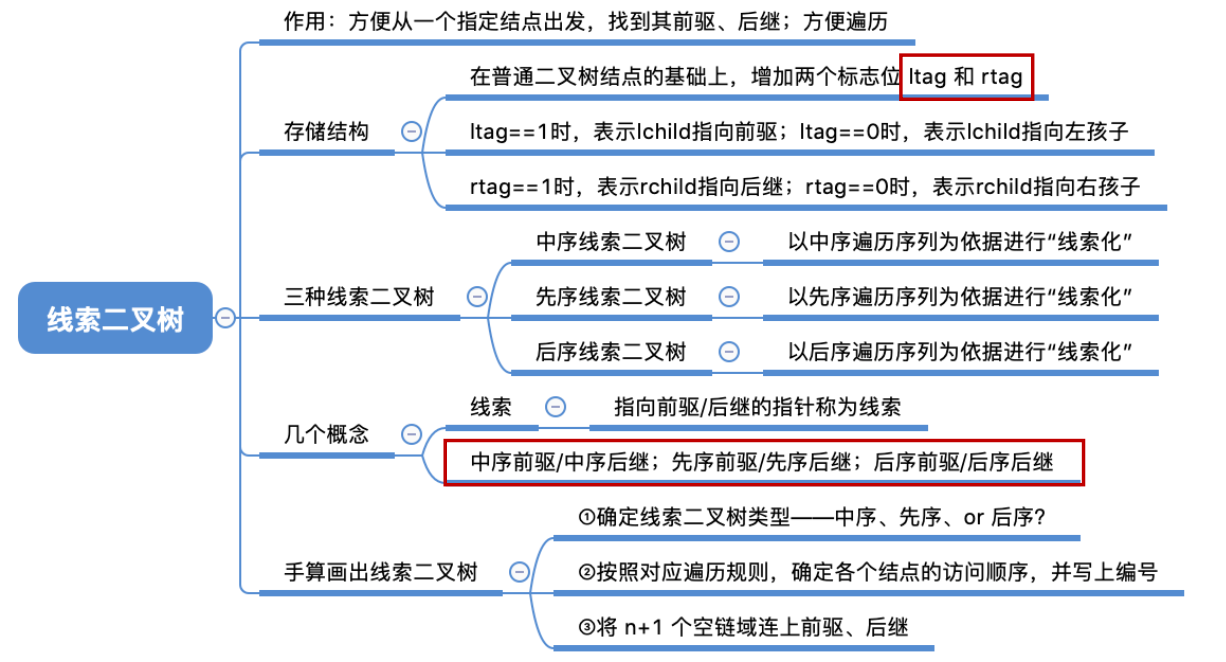
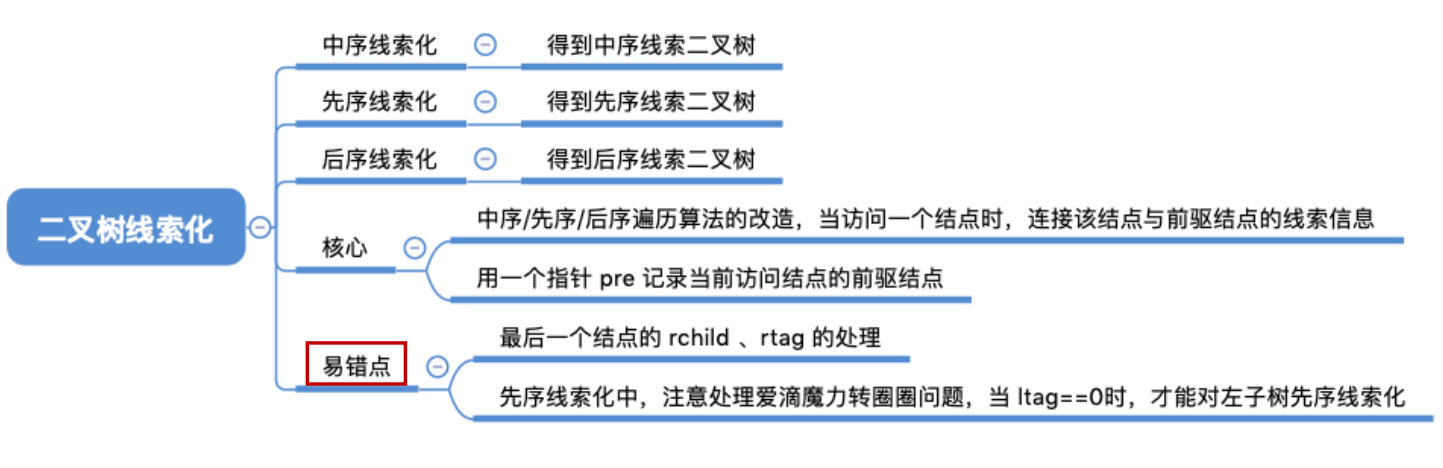
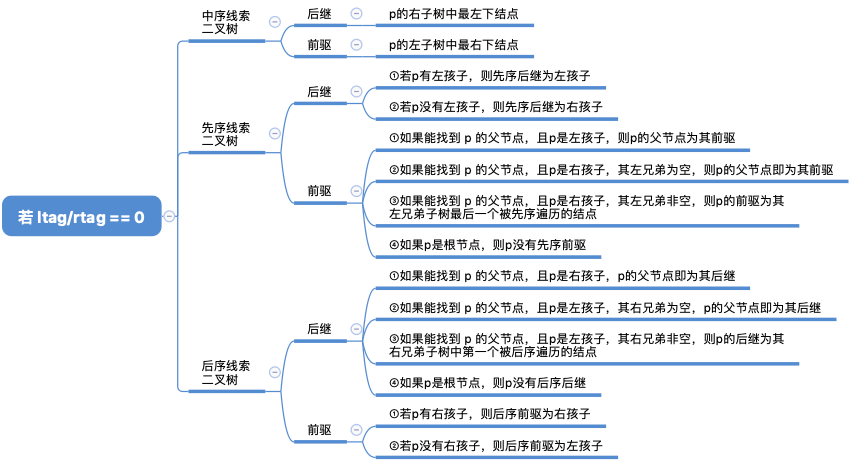
1、基本概念

普通二叉树只能找到结点的左右孩子信息，而该结点的直接前驱和直接后继只能在遍历过程中获得，

若将遍历后对应的有关前驱和后继预存起来，则从第一个结点开始就能很快“顺藤摸瓜”而遍历整个树。

思路：

若结点有左子树，则lchild指向其左孩子；否则，lchild指向其直接前驱(即线索)；

若结点有右子树，则rchild指向其右孩子；否则，rchild指向其直接后继(即线索) 。

LTag： 若 LTag=0, lchild域指向左孩子；

​ 若 LTag=1, lchild域指向其前驱。

RTag： 若 RTag=0, rchild域指向右孩子；

​ 若 RTag=1, rchild域指向其后继。

线索二叉树的遍历

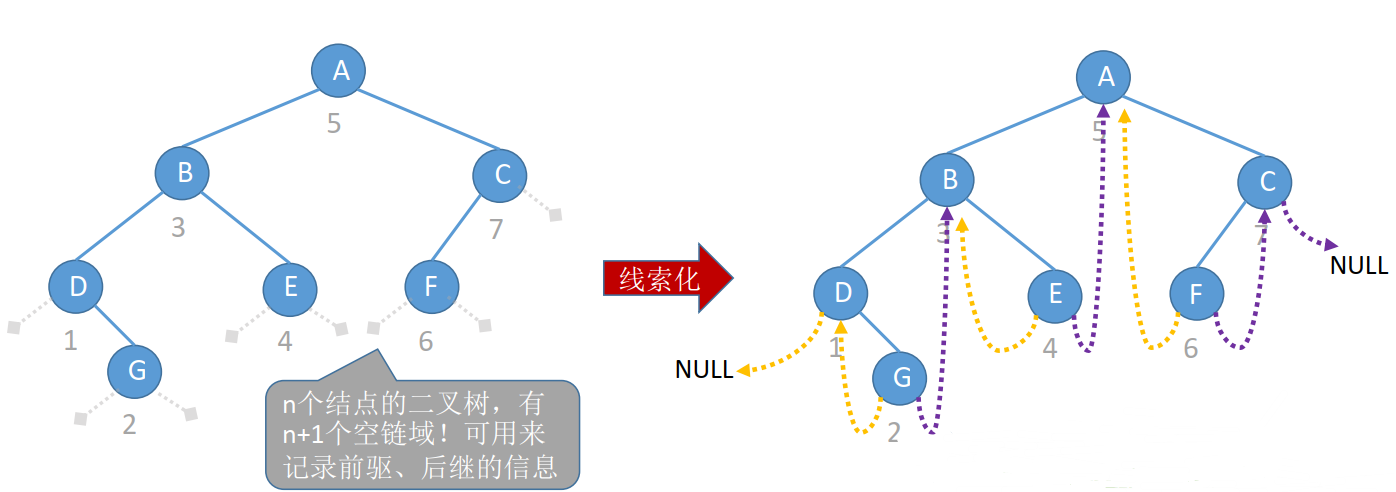
2、中序线索二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
#include <iostream>
#include <string>
using namespace std;

typedef struct ThreadNode {
    int value;
    struct ThreadNode *lChild, *rChild;
    int lTag, rTag;  //左右线索标志
    //tag == 0 表示孩子
    //tag == 1 表示线索
}ThreadNode, *ThreadTree;
ThreadNode  *pre = nullptr;  //全局变量pre，指当前访问结点的前驱

/**
 * 创建二叉树
 * @param root
 */
void CreateBinaryTree(ThreadTree &root) {
    auto *node1 = (ThreadNode *)malloc(sizeof(ThreadNode));
    auto *node2 = (ThreadNode *)malloc(sizeof(ThreadNode));
    auto *node3 = (ThreadNode *)malloc(sizeof(ThreadNode));
    auto *node4 = (ThreadNode *)malloc(sizeof(ThreadNode));
    auto *node5 = (ThreadNode *)malloc(sizeof(ThreadNode));
    auto *node6 = (ThreadNode *)malloc(sizeof(ThreadNode));
    root->rTag = 0;  root->lTag = 0;
    node1->rTag = 0; node1->lTag = 0;
    node2->rTag = 0; node2->lTag = 0;
    node3->rTag = 0; node3->lTag = 0;
    node4->rTag = 0; node4->lTag = 0;
    node5->rTag = 0; node5->lTag = 0;
    node6->rTag = 0; node6->lTag = 0;
    root->value = 15;
    node1->value = 10;
    node2->value = 23;
    node3->value = 8;
    node4->value = 12;
    node5->value = 21;
    node6->value = 9;
    //
    root->lChild = node1;
    root->rChild = node2;
    //
    node1->lChild = node3;
    node1->rChild = node4;
    node2->lChild = node5;
    node2->rChild = nullptr;
    //
    node3->lChild = nullptr;
    node3->rChild = node6;
    node4->lChild = nullptr;
    node4->rChild = nullptr;
    node5->rChild = nullptr;
    node5->lChild = nullptr;
    //
    node6->lChild = nullptr;
    node6->rChild = nullptr;
}

/**
 * 访问根结点
 * @param p
 */
void visit(ThreadNode *p) {
    if (p->lChild == nullptr) {  //如果左子树为空，建立前驱线索
        p->lChild = pre; //左孩子设为前驱结点
        p->lTag = 1;  //左标志设为1，代表有线索
    }
    if (pre != nullptr && pre->rChild == nullptr) { //如果右子树为空，建立前驱结点的后继线索
        pre->rChild = p;  //前驱节点的后继线索
        pre->rTag = 1; //右标志设为1，代表有线索
    }
    pre = p; //前驱结点更换
}

/**
 * 中序遍历二叉树，一边遍历一遍线索化； 左根右遍历
 * @param p 根结点
 */
void InThread(ThreadTree &p) {
    if (p == nullptr) { //结点为空返回
        return;
    }
    InThread(p->lChild); //中序遍历左子树
    visit(p); //根节点线索化
    InThread(p->rChild); //中序遍历右子树
}


/**
 * 中序线索化二叉树
 * @param root
 * @return
 */
bool CreatInThread(ThreadTree &root) {
    //根节点不为空
    if (root != nullptr) {
        InThread(root);  //中序线索化二叉树
        if (pre->rChild == nullptr)  //处理遍历的最后一个结点
            pre->rTag = 1;
    }
}


/**
 * 中序获得首一个结点
 * @param p
 * @return
 */
ThreadNode *FirstInNode(ThreadNode *p) {
    while (p->lTag == 0) { //最左下结点
        p = p->lChild;
    }
    return p;
}

/**
 * 中序获得下一个一个结点
 * @param p
 * @return
 */
ThreadNode *NextInNode(ThreadNode *p) {
    if (p->rTag == 0) {
        return FirstInNode(p->rChild);
    }else { //rTag == 1,直接返回后继线索
        return p->rChild;
    }
}

/**
 * 中序线索二叉树的遍历
 * @param root
 */
void InOrder(ThreadNode *root) {
    for (ThreadNode *p = FirstInNode(root); p != nullptr ; p = NextInNode(p)) {
        cout << p->value << "->";
    }
}


int main() {
    ThreadTree root;
    root = (ThreadNode *)malloc(sizeof(ThreadNode));
    cout << "初始化创建二叉树" <<  endl;
    CreateBinaryTree(root);
    //
    cout << "中序遍历线索化" <<  endl;
    CreatInThread(root);
    cout << "中序线索化二叉树的中序遍历" << endl;
    InOrder(root);
    return 0;
}
1
2
3
4
初始化创建二叉树
中序遍历线索化
中序线索化二叉树的中序遍历
8->9->10->12->15->21->23->

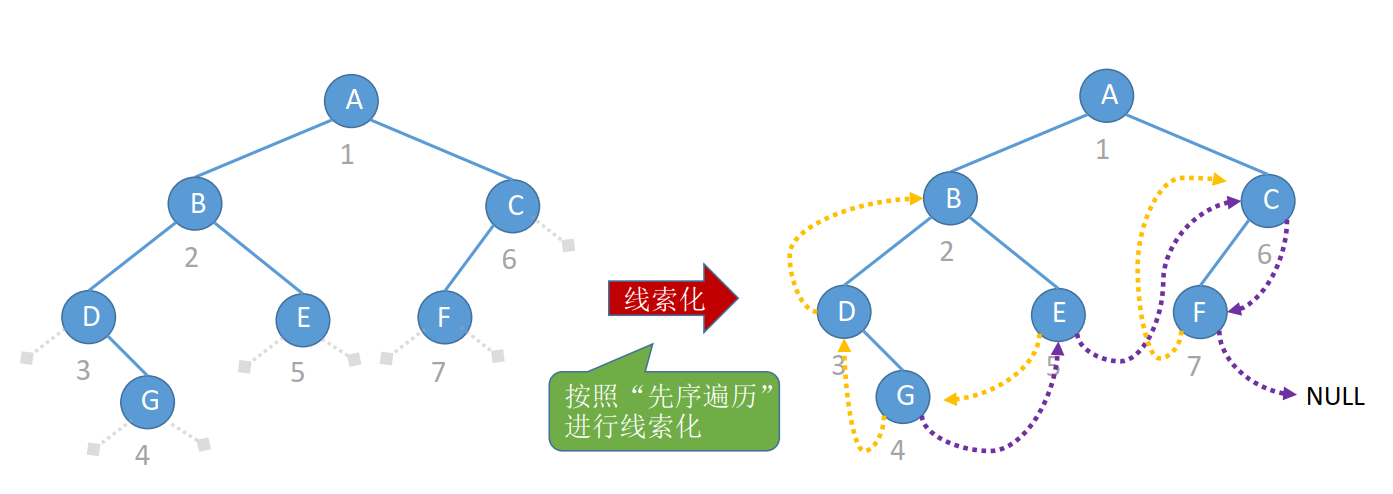
3、先序线索二叉树

思路： 找后继遍历先序线索二叉树

  1. 若p->rTag == 1，则next = p->rChild

  2. 若p->rTag == 0

    ① 若有左孩子，则先序后继为左孩子

    ② 若没有左孩子，则先序后继为右孩子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
//数据结构定义看上面中序线索二叉树代码

/**
 * 访问根结点
 * @param p
 */
void visit(ThreadNode *p) {
    if (p->lChild == nullptr) {  //如果左子树为空，建立前驱线索
        p->lChild = pre; //左孩子设为前驱结点
        p->lTag = 1;  //左标志设为1，代表有线索
    }
    if (pre != nullptr && pre->rChild == nullptr) { //如果右子树为空，建立前驱结点的后继线索
        pre->rChild = p;  //前驱节点的后继线索
        pre->rTag = 1; //右标志设为1，代表有线索
    }
    pre = p; //前驱结点更换
}

/**
 * 先序遍历二叉树，一边遍历一遍线索化；根左右遍历
 * @param p
 */
void PreThread(ThreadTree &p) {
    if (p != nullptr) { //结点非空
        visit(p); //根节点线索化
        if (p->lTag == 0) //左子树不是前驱线索
            PreThread(p->lChild); //先序遍历左子树
        if (p->rTag == 0) //右子树不是前驱线索
            PreThread(p->rChild); //先序遍历右子树
    }
}


/**
 * 先序线索化二叉树
 * @param root
 * @return
 */
bool CreatPreThread(ThreadTree &root) {
    //
    if (root != nullptr) {
        PreThread(root);  //先序线索化二叉树
        if (pre->rChild == nullptr)  //处理遍历的最后一个结点
            pre->rTag = 1;
    }
}

/**
 * 先序获得下一个结点
 * @param p
 * @return
 */
ThreadNode *NextPreNode(ThreadNode *p) { //
    if (p->rTag == 1) { //如果rTag == 1,有直接后继，返回直接后继
        return p->rChild;
    }else { //没有
        if (p->lTag == 0) { //无左标志线索，有孩子
            return p->lChild; //返回左孩子
        }else { //有左标志线索
            return p->rChild;  //返回右孩子
        }
    }
}

/**
 * 先序线索二叉树的遍历
 * @param root
 */
void PreOrder(ThreadNode *root) {
    for (ThreadNode *p = root; p != nullptr; p = NextPreNode(p)) {
        cout << p->value << "->";
    }
}
1
2
3
4
初始化创建二叉树
先序遍历线索化
先序线索化二叉树的先序遍历
15->10->8->9->12->23->21->

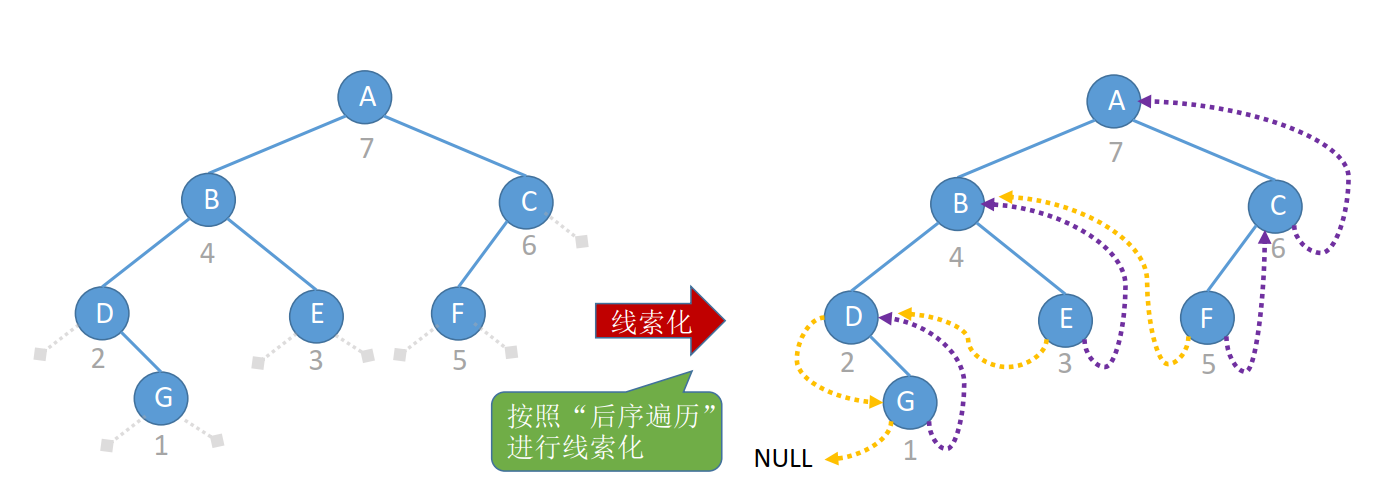
4、后序线索二叉树

思路： 找前驱遍历后序线索二叉树

  1. 若p->rLag == 1，则pre = p->lChild

  2. 若p->lTag == 0

    ① 若有右孩子，则后序前驱为右孩子

    ② 若有左孩子，则后序前驱为左孩子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
//数据结构定义看上面中序线索二叉树代码

/**
 * 访问根结点
 * @param p
 */
void visit(ThreadNode *p) {
    if (p->lChild == nullptr) {  //如果左子树为空，建立前驱线索
        p->lChild = pre; //左孩子设为前驱结点
        p->lTag = 1;  //左标志设为1，代表有线索
    }
    if (pre != nullptr && pre->rChild == nullptr) { //如果右子树为空，建立前驱结点的后继线索
        pre->rChild = p;  //前驱节点的后继线索
        pre->rTag = 1; //右标志设为1，代表有线索
    }
    pre = p; //前驱结点更换
}

/**
 * 后序遍历二叉树，一边遍历一遍线索化；左右根遍历
 * @param p
 */
void PostThread(ThreadTree &p) {
    if (p == nullptr) { //结点为空返回
        return;
    }
    PostThread(p->lChild); //后序遍历左子树
    PostThread(p->rChild); //后序遍历右子树
    visit(p); //根节点线索化
}


/**
 * 后序线索化二叉树
 * @param root
 * @return
 */
bool CreatPostThread(ThreadTree &root) {
    //
    if (root != nullptr) {
        PostThread(root);  //后序线索化二叉树
        if (pre->rChild == nullptr)  //处理遍历的最后一个结点
            pre->rTag = 1;
    }
}

/**
 * 后序获得最后一个结点
 * @param p
 * @return
 */
ThreadNode *LastPostNode(ThreadNode *p) {
    return p;
}

/**
 * 后序获得上一个一个结点
 * @param p
 * @return
 */
ThreadNode *PrePostNode(ThreadNode *p) {
    if (p->lTag == 1) { //有直接前驱
        return p->lChild;
    }else { //lTag == 0 无直接前驱
        if (p->rChild != nullptr && p->rTag == 0) { //如果右孩子存在，且rTag==0,则右孩子为直接前驱
            return LastPostNode(p->rChild);
        }else if (p->lChild != nullptr && p->lTag == 0) { //如果左孩子存在，且rTag==0,则左孩子为直接前驱
            return LastPostNode(p->lChild);
        }
    }
}

/**
 * 后序线索二叉树的遍历
 * @param root
 */
void PostOrder(ThreadNode *root) {
    for (ThreadNode *p = LastPostNode(root); p != nullptr ; p = PrePostNode(p)) {
        cout << p->value << "->";
    }
}

int main() {
    ThreadTree root;
    root = (ThreadNode *)malloc(sizeof(ThreadNode));
    cout << "初始化创建二叉树" <<  endl;
    CreateBinaryTree(root);
    cout << "后序遍历线索化" <<  endl;
    CreatPostThread(root);
    cout << "后序线索化二叉树的先序遍历" << endl;
    PostOrder(root);
    return 0;
}
1
2
3
4
初始化创建二叉树
后序遍历线索化
后序线索化二叉树的先序遍历
15->23->21->10->12->8->9->
北以晨光 wechat
欢迎您扫一扫上面的微信公众号，订阅我的博客！
------ 本文结束感谢您的阅读 ------
相关文章