1 数据结构-树和二叉树(四)树和森林
1.1 树的逻辑结构
树是n(n≥0)个结点的有限集合, n = 0时,称为空树,这是一种特殊情况。
在任意一棵非空树中应满足:
1、有且仅有一个特定的称为根的结点。
2、当n > 1时,其余结点可分为m(m > 0)个互不相交的有限集合T1, T2,…, Tm,其中每个集合本身又是一棵树,并且称为根结点的子树。
树的定义是递归的,即在树的定义中又用到了其自身,树是一种递归的数据结构。
树作为一种逻辑结构,同时也是一种分层结构,具有以下两个特点:
- 🌲除了根节点外,任何一个结点都有且仅有一个前驱
- 🌳中所有结点可以有零个或多个后继
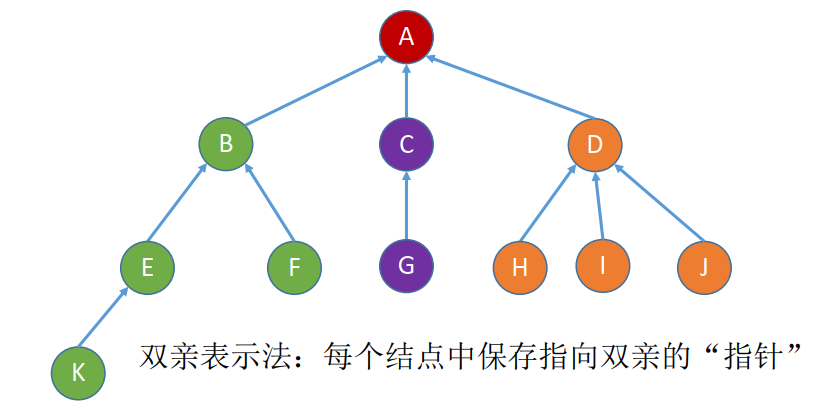
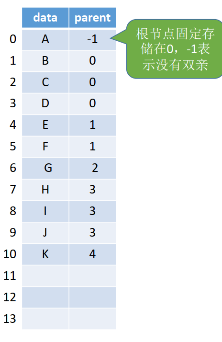
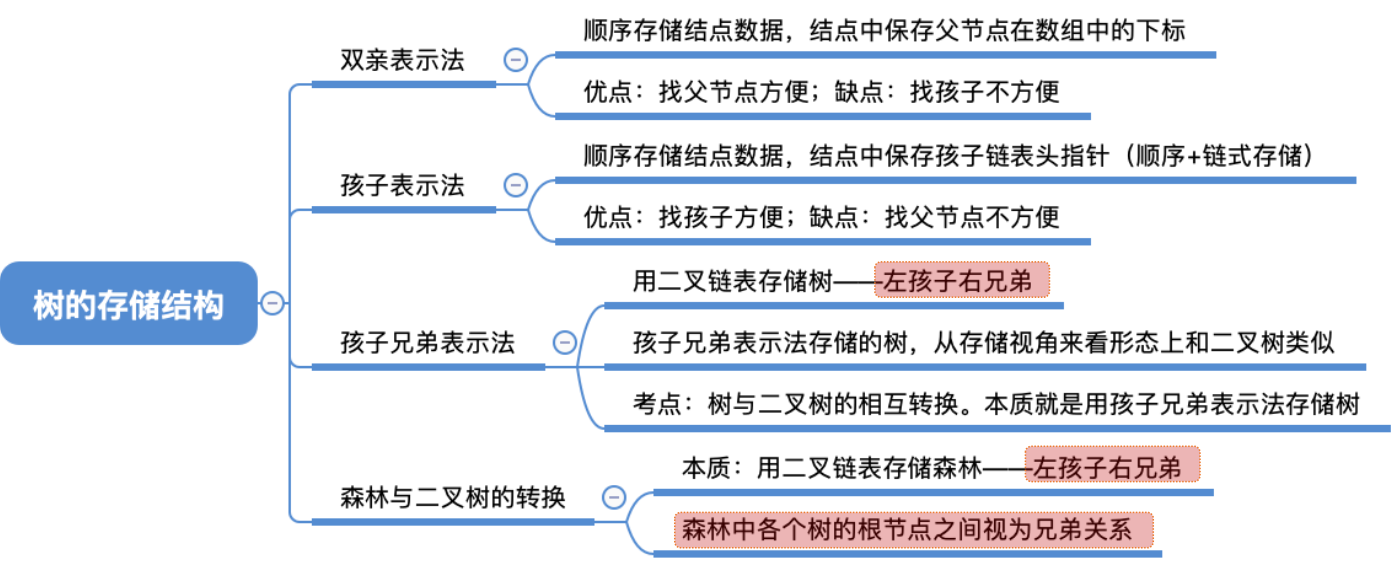
1.2 双亲表示法
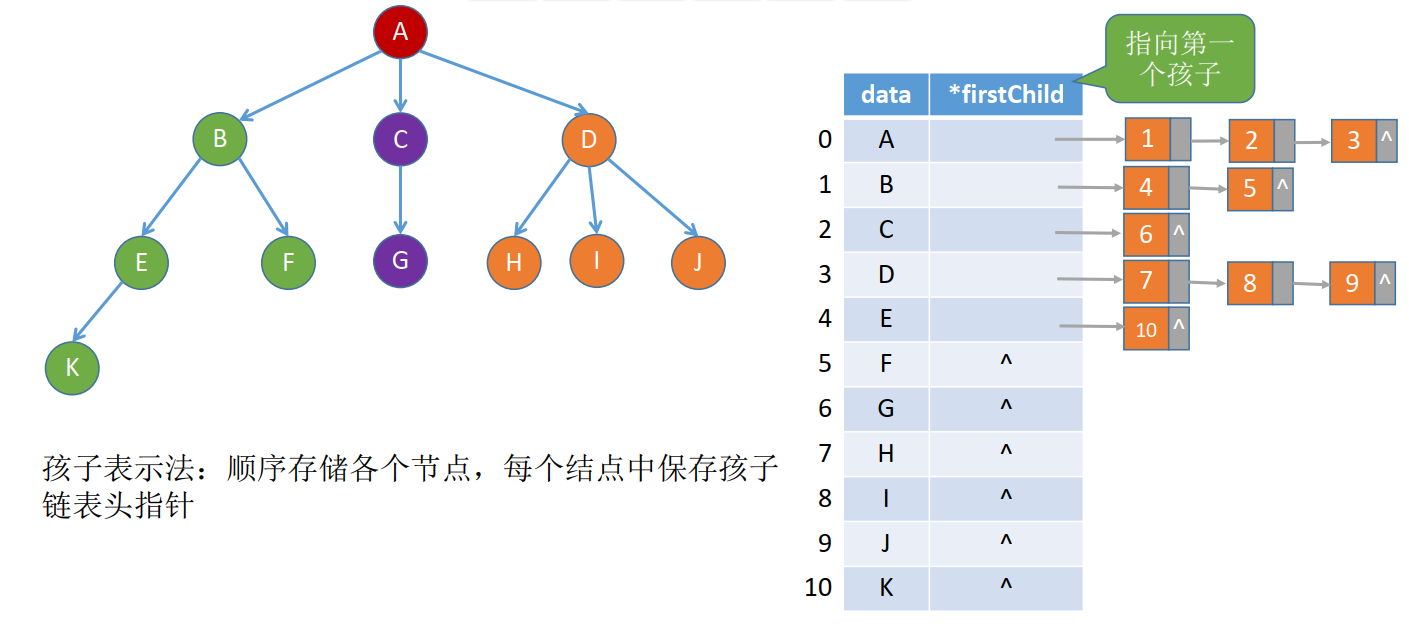
1.3 孩子表示法
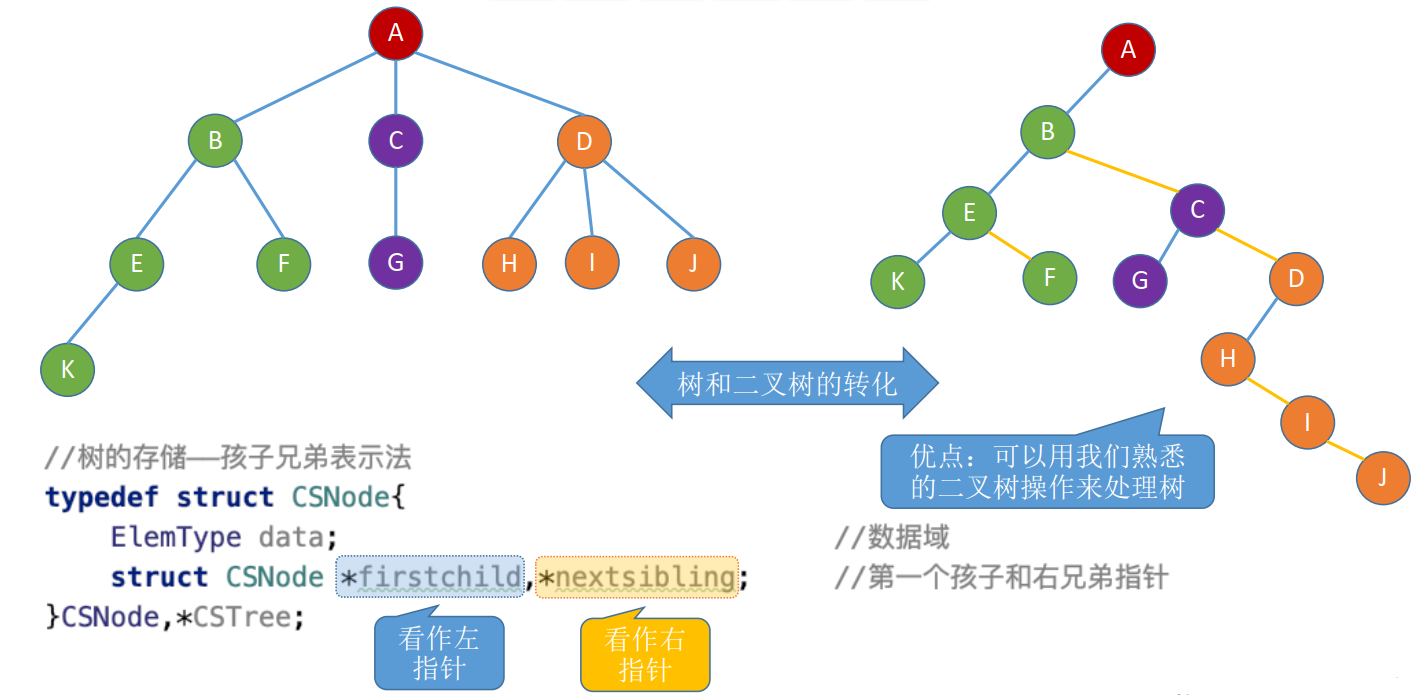
1.4 孩子兄弟表示法
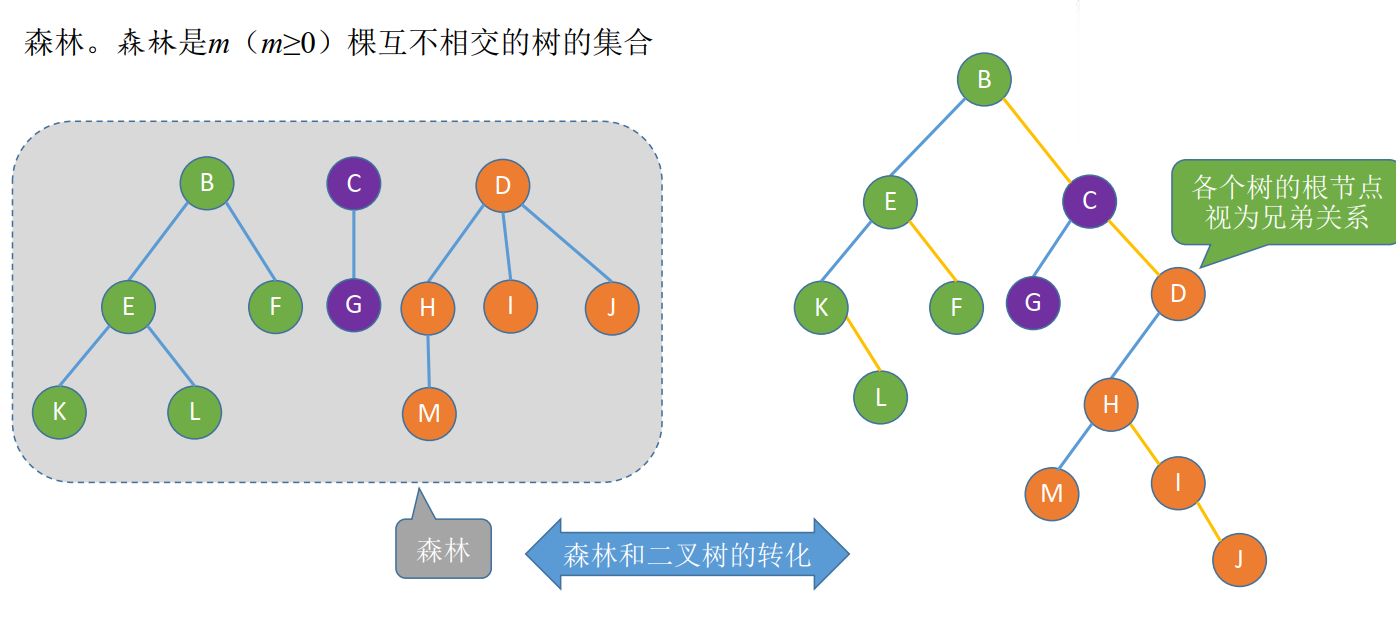
1.5 树、森林与二叉树的转换
1.6 树和森林的遍历
1、树的遍历
(1)先根遍历
先根遍历。若树非空,先访问根结点,再依次对每棵子树进行先根遍历。 深度优先遍历
树的先根遍历序列与这棵树相应二叉树的先序序列相同
(2)后根遍历
后根遍历。若树非空,先依次对每棵子树进行后根遍历,最后再访问根结点。 深度优先遍历
树的后根遍历序列与这棵树相应二叉树的中序序列相同。
(3)层次遍历
层次遍历(用队列实现) 广度优先遍历
① 若树非空, 则根节点入队
② 若队列非空,队头元素出队并访问,同时将该元素的孩子依次入队
③ 重复②直到队列为空
2、森林的遍历
(1)先序遍历
先序遍历森林。
若森林为非空,则按如下规则进行遍历:
- 访问森林中第一棵树的根结点。
- 先序遍历第一棵树中根结点的子树森林。
- 先序遍历除去第一棵树之后剩余的树构成的森林
效果等同于依次对各个树进行先根遍历 ,等同于依次对二叉树的先序遍历
(2)中序遍历
中序遍历森林。
若森林为非空,则按如下规则进行遍历:
- 中序遍历森林中第一棵树的根结点的子树森林。
- 访问第一棵树的根结点。
- 中序遍历除去第一棵树之后剩余的树构成的森林。
效果等同于依次对各个树进行后根遍历 ,等同于依次对二叉树的中序遍历