数据结构-排序(一)绪论
排序(Sort) ,就是重新排列表中的元素,使表中的元素满⾜按关键字有序的过程。
输入: n个记录$R_1, R_2,…, R_n$,对应的关键字为$k_1, k_2,…, k_n。$
输出:输⼊序列的⼀个重排$R_1ʹ, R_2ʹ,…, R_nʹ,$使得有$k_1ʹ≤k_2ʹ≤…≤k_nʹ$(也可递减)
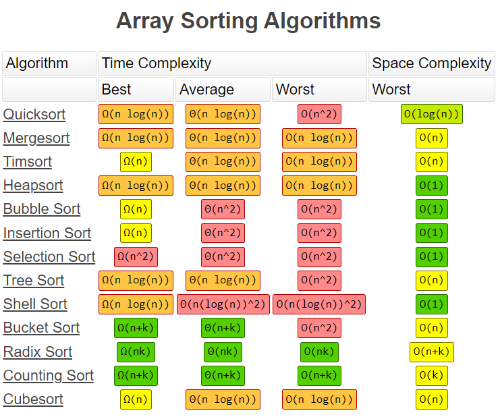
排序算法的评价指标:①时间复杂度;②空间复杂度
算法的稳定性: 若待排序表中有两个元素$ R_i$ 和$ R_j$,其对应的关键字相同即$key_i= key_j$,且在排序前的前⾯$ R_i$ 和$ R_j$,若使⽤某⼀排序算法排序后, $ R_i$ 仍然在 $ R_j$的前面,则称这个排序算法是稳定的,否则称排序算法是不稳定的。
分类:
- 内部排序:数据都在内存里(关注如何使算法时、空复杂度更低 )
- 外部排序:数据太多,无法全部存在内存里(还要关注如何使读/写磁盘次数更少)
| 算法 | 时间复杂度 | 空间复杂度 | 稳定性 | ||
|---|---|---|---|---|---|
| 最好 | 最差 | 平均 | |||
| 直接插入排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 稳定 |
| 折半插入排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 稳定 |
| 希尔排序 | 不确定 | $O(n^2)$ | $O(n^{1.25})~O(1.6n^{1.25})$ | $O(1)$ | 不稳定 |
| 冒泡排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 稳定 |
| 快速排序 | $O(nlog_2n)$ | $O(n^2)$ | $O(nlog_2n)$ | $O(log_2n)$ | 不稳定 |
| 简单选择排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 不稳定 |
| 堆排序 | $O(nlog_2n)$ | $O(nlog_2n)$ | $O(nlog_2n)$ | $O(1)$ | 不稳定 |
| 归并排序 | $O(nlog_2n)$ | $O(nlog_2n)$ | $O(nlog_2n)$ | $O(n)$ | 稳定 |
| 基数排序 | $O(d(n+rd))$ | $O(d(n+rd))$ | $O(d(n+rd))$ | $O(n+rd)$ | 稳定 |
时间空间复杂度网站推荐:https://www.bigocheatsheet.com/