数据结构-排序（二）插入排序

一、 直接插入排序

1、算法思想

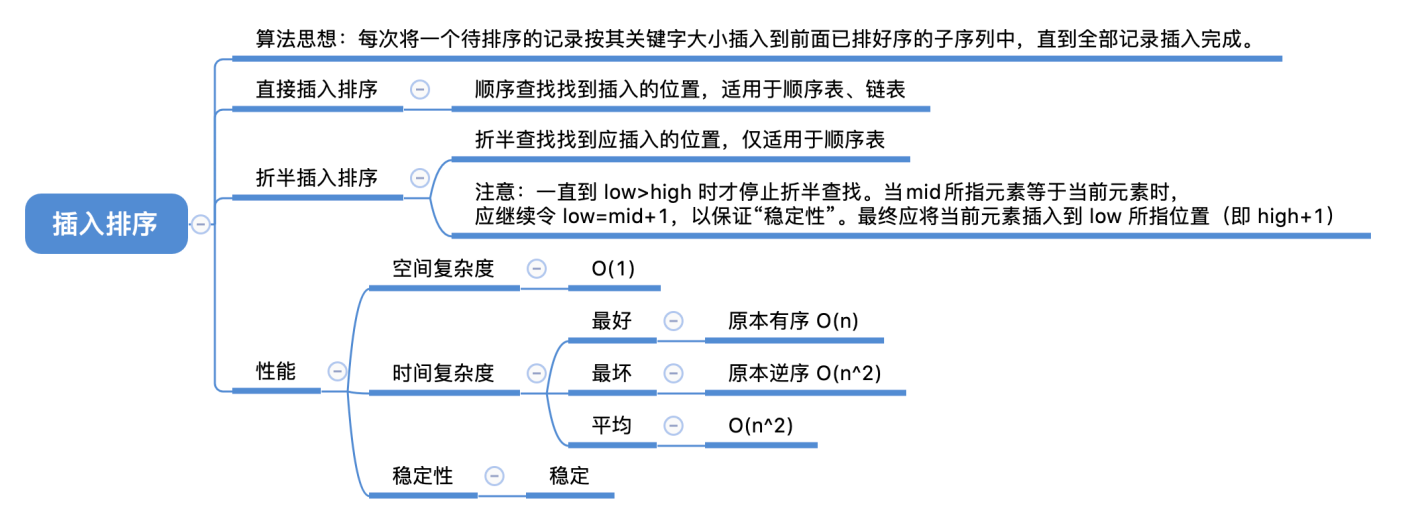
算法思想： 每次将⼀个待排序的记录按其关键字大小插入到前面已排好序的子序列中，直到全部记录插⼊完成。

排序过程：

• 整个排序过程为n-1趟插入，
• 先将序列中第1个记录看成是一个有序子序列，
• 然后从第2个记录开始，逐个进行插入，直至整个序列有序。

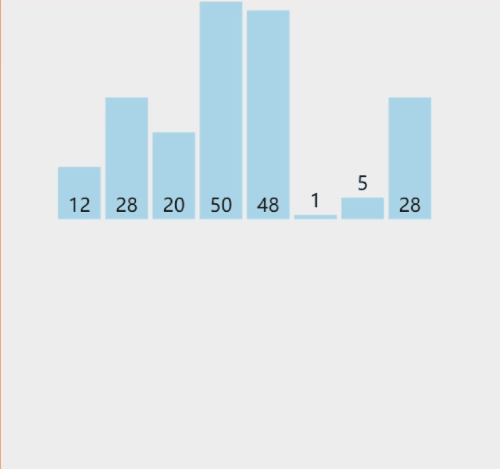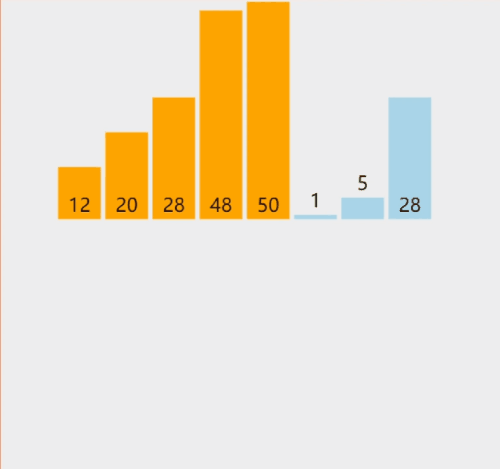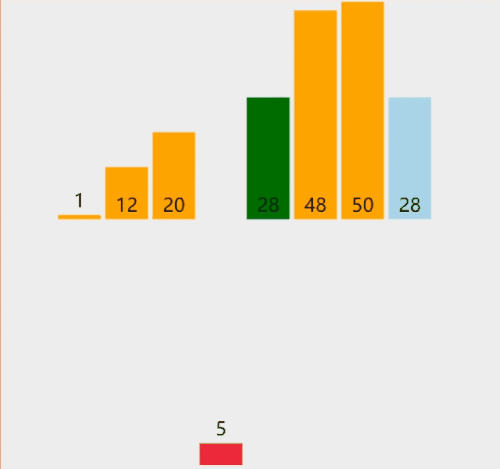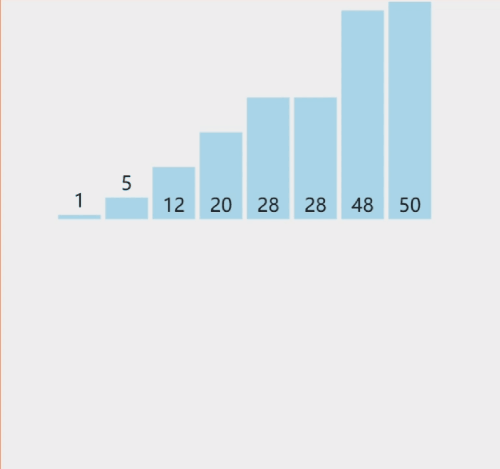
以上gif动图制作，图像来自网站：VisuAlgo

链表实现请参考：链表实现直接插入排序

2、代码实现

#include <iostream>
#include <string>
using namespace std;

/**
 * 插入排序
 * @param arr  数组
 * @param n  数据个数
 * @return 
 */
bool InsertSort(int arr[], int n) {
    for (int i = 1; i < n; i++) {
        if (arr[i] < arr[i - 1]) { //若关键字小于前驱
            int t = arr[i]; //暂存关键字
            int j;
            for (j = i - 1; j >= 0 && arr[j] > t ; j--) { //检查前面排序的元素
                arr[j + 1] = arr[j]; //所有大于t的元素完后挪位
            }
            arr[j + 1] = t; //复制到插入位置
        }
    }
}

/**
 * 输出数组
 * @param arr 
 * @param n 
 */
void PrintArray(int arr[], int n) {
    for (int i = 0; i < n; i++) {
        cout << arr[i] << "  ";
    }
    printf("\n");
}
int main() {
    int arr[] = {12, 28, 20, 50, 48, 1, 5, 28};
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << "输出初始数组" << endl;
    PrintArray(arr, n);
    cout << "直接插入排序" << endl;
    InsertSort(arr, n);
    cout << "输出排序后数组" << endl;
    PrintArray(arr, n);
    return 0;
}

输出初始数组
12  28  20  50  48  1  5  28
直接插入排序
输出排序后数组
1  5  12  20  28  28  48  50

3、算法效率分析

1、空间复杂度： O(1)

2、时间复杂度： 主要来自对比关键字、移动元素若有 n 个元素，则需要 n-1 趟处理

最好情况：共n-1趟处理，每⼀趟只需要对比关键字1次，不⽤移动元素

最好时间复杂度—— O(n)

最坏情况：
第1趟：对比关键字2次，移动元素3次
第2趟：对比关键字3次，移动元素4次
…
第 i 趟：对比关键字 i+1次，移动元素 i+2 次

最坏时间复杂度——$O(n^2)$

最好时间复杂度（全部有序）：O(n)

最坏时间复杂度（全部逆序）：$O(n^2)$

平均时间复杂度：$O(n^2)$

3、算法稳定性： 稳定

二、折半插入排序

1、算法思想

算法思想： 先用折半查找找到应该插⼊的位置，再移动元素

• 当 low > high 时折半查找停止，应将 [low, i-1] 内的元素全部右移，并将 A[0] 复制到 low 所指位置
• 当 A[mid] == A[0] 时，为了保证算法的“稳定性”，应继续在 mid 所指位置右边寻找插入位置

2、代码实现

/**
 * 折半插入排序
 * @param arr
 * @param n
 * @return
 */
bool SplitInsertSort(int arr[], int n ) {
    for (int i = 2; i <= n ; i++) {
        arr[0] = arr[i]; //暂存关键字
        int low = 1, high = i - 1; //折半查找范围
        while (low <= high) { //折半查找
            int mid = (low + high) / 2;
            if (arr[mid] > arr[0]) { //查找左子表
                high = mid - 1;
            }else { //查找右半子表
                low = mid + 1;
            }
        }
        for (int j = i - 1; j >= high + 1 ; --j) {
            arr[j + 1] = arr[j]; //统一后移操作，空出插入位置
        }
        arr[high + 1] = arr[0]; //插入操作
    }
}

3、算法效率分析

1、空间复杂度： O(1)

2、时间复杂度：

比起“直接插⼊排序”，比较关键字的次数减少了，但是移动元素的次数没变，整体来看时间复杂度依然是$O(n^2)$

3、算法稳定性： 稳定