数据结构-排序（六）简单选择排序

一、算法思想

选择排序算法思想： 每⼀趟在待排序元素中选取关键字最小（或最大）的元素加入有序子序列。n个元素的简单选择排序需要 n-1 趟处理

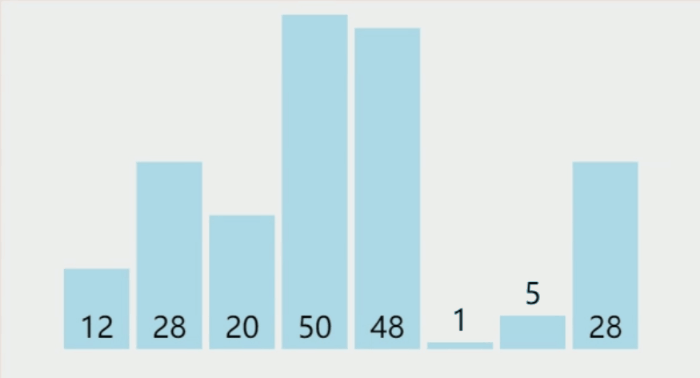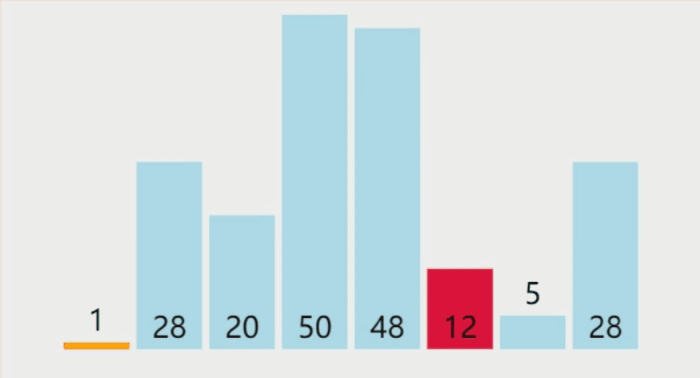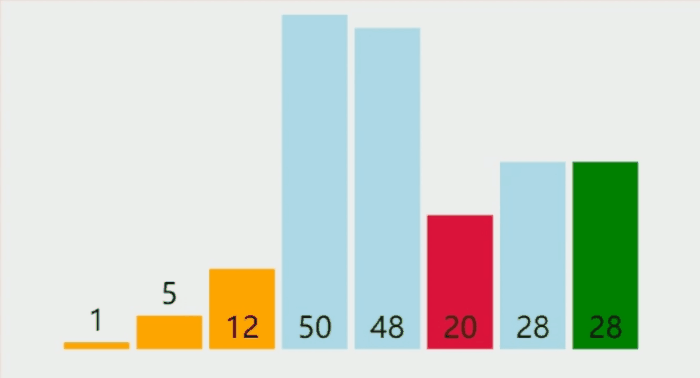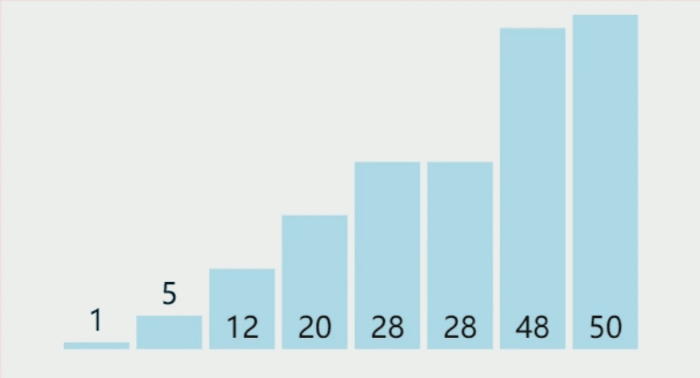
以上gif动图制作，图像来自网站：VisuAlgo

二、代码实现

#include <iostream>
#include <string>
using namespace std;

/**
 * 简单选择排序
 * @param arr
 * @param n
 */
void SelectSort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) { //n - 1趟
        int min = i; //记录最小元素位置
        for (int j = i + 1; j < n; j++) { //再arr[i...n-1]中选择最小元素
            if (arr[j] < arr[min]) { //更新最小位置
                min = j;
            }//if
        }//for
        if (min != i) { //交换最小值
            swap(arr[i], arr[min]); //交换顺序
        }
    }//for
}
/**
 * 输出数组
 * @param arr
 * @param n
 */
void PrintArray(int arr[], int n) {
    for (int i = 0; i < n; i++) {
        cout << arr[i] << "  ";
    }
    printf("\n");
}
int main() {
    int arr[] = {12, 28, 20, 50, 48, 1, 5, 28};
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << "输出arr初始数组" << endl;
    PrintArray(arr, n);
    cout << "arr简单选择排序" << endl;
    SelectSort(arr, n);c
    cout << "输出arr排序后数组" << endl;
    PrintArray(arr, n);
    return 0;
}

三、算法效率分析

1、空间复杂度： O(1)

2、时间复杂度

⽆论有序、逆序、还是乱序，⼀定需要 n-1 趟处理

比较次数 = (n - 1) + (n - 2 )+…+ 1 = $\frac{n(n-1)}{2}$ ；交换次数 < n - 1；

时间复杂度：$O(n^2)$

3、稳定性： 不稳定

4、适⽤性： 既可以用于顺序表，也可用于链表