0%

前缀、中缀、后缀表达式

发表于 分类于
本文字数： 5.7k 阅读时长 ≈ 5 分钟

前缀、中缀、后缀表达式

一、前缀表达式

前缀表达式是一种没有括号的算术表达式，与中缀表达式不同的是，其将运算符写在前面，操作数写在后面。也被叫做波兰表达式,比如（499 + 1）* 2 + 314 的前缀表达式为 + * + 499 1 2 314

前缀表达式的计算机求值

求值方法：

从右至左扫描表达式，遇到数字时，将数字压入栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（栈顶元素 和 次顶元素），并将结果入栈；重复上述过程直到表达式最左端，最后运算得出的值即为表达式的结果

举栗子🌰🌰（499 + 1）* 2 + 314 对应的前缀表达式就是 + * + 499 1 2 314, 针对前缀表达式求值步骤如下:

  1. 从右至左扫描，将314、2、1、499压入堆栈
  2. 遇到+运算符，因此弹出499和1（499为栈顶元素，1为次顶元素），计算499 + 1的值，得500，再将500入栈
  3. 接下来是 * 运算符，因此弹出500和2（500为栈顶元素，2为次顶元素），计算500 * 2的值，得1000，再将1000入栈
  4. 最后是+运算符，计算出1000 + 314的值，即1314💝💝，由此得出最终结果

二、中缀表达式

中缀表达式是一个通用的算术或逻辑公式表示方法， 操作符是以中缀形式处于操作数的中间，中缀表达式是人们常用的算术表示方法，比如（499 + 1）* 2 + 314

中缀表达式的计算机求值

可看另一篇文章，栈实现中缀表达式计算机

栈实现中缀表达式计算机

三、后缀表达式

逆波兰式（或逆波兰记法），也叫后缀表达式，其将运算符写在操作数之后，后缀表达式源自于前缀表达式，为了区分前缀和后缀表示，通常将后缀表示称为逆波兰表示。比如：（499 + 1）x 2 + 314 的后缀表达试为 499 1 + 2 x 314 +

后缀表达式的计算机求值

求值方法：

从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素 和 栈顶元素），并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果。

举栗子🌰🌰（499 + 1）* 2 + 314 对应的后缀表达式就是 499 1 + 2 * 314 +, 针对前缀表达式求值步骤如下:

  1. 从左至右扫描，将499和1压入堆栈；
  2. 遇到+运算符，因此弹出499和1（1为栈顶元素，499为次顶元素），计算出499+1的值，得500，再将500入栈；
  3. 将2入栈；
  4. 接下来是 * 运算符，因此弹出500和2，计算出500 * 2，得1000，再将1000入栈；
  5. 将314入栈；
  6. 最后是+运算符，计算出1000+314的值，即1314💗💗，由此得出最终结果

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Stack;

public class PolandNotation {
    public static void main(String[] args) {
        //先定义逆波兰表达式
        //(3+4)×5-6 对应的后缀表达式就是 3 4 + 5 * 6 -
        String suffixExpression = "499 1 + 2 * 314 +";
        //思路
        //1、先将"3 4 + 5 × 6 -" 放到ArrayList中
        //2、将ArrayList 传递一个方法，遍历ArrayList 配合栈 完成计算

        List<String> list = getListString(suffixExpression);

        int res = calculate(list);
        System.out.println("计算的结果是： " + res);
    }

    //将一个逆波兰表达式，依次将数据和运算符 放入到ArrayList中
    public static List<String> getListString(String suffixExpression) {
        //将suffixExpression 分割
        String[] split = suffixExpression.split(" ");
        List<String> list = new ArrayList<String>();
        //Collections.addAll(list, split);
        for (String element: split)
            list.add(element);
        return list;
    }

    //完成逆波兰表达式的计算
    /*
    1. 从左至右扫描，将499和1压入堆栈；
	2. 遇到+运算符，因此弹出499和1（1为栈顶元素，499为次顶元素），
	计算出499+1的值，得500，再将500入栈；
	3. 将2入栈；
	4. 接下来是×运算符，因此弹出500和2，计算出500×2，得1000，再将1000入栈；
	5. 将314入栈；
	6. 最后是+运算符，计算出1000+314的值，即1314💗💗，由此得出最终结果	
     */

    public static int calculate(List<String> ls) {
        //创建栈，只需要一个栈
        Stack<String> stack = new Stack<String>();
        //遍历ls
        for (String item: ls) {
            //这里使用正则表达式来取出数
            if (item.matches("\\d+")) { //匹配多位数
                //入栈
                stack.push(item);
            } else {
                //pop出两个数，并运算，再入栈
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int res = 0;
                if (item.equals("+")) {
                    res = num1 + num2;
                } else if (item.equals("-")) {
                    res = num1 - num2;
                } else if (item.equals("*")) {
                    res = num1 * num2;
                } else if (item.equals("/")) {
                    res = num1 / num2;
                } else {
                    throw new RuntimeException("运算符有误");
                }
                //把res入栈
                stack.push("" + res);
            }
        }
        //返回最后栈顶的结果
        return Integer.parseInt(stack.pop());
    }
}

结果展示：

1
计算的结果是： 1314

中缀表达式转为后缀表达式

转换算法步骤📋👇

  1. 初始化两个栈：运算符栈s1和储存中间结果的栈s2；

  2. 从左至右扫描中缀表达式；

  3. 遇到操作数时，将其压s2栈；

  4. 遇到运算符时，比较其与s1栈顶运算符的优先级：

    4.1.如果s1为空，或栈顶运算符为左括号“ ( ”，则直接将此运算符入栈；

    4.2.否则，若优先级比栈顶运算符的高，也将运算符压入s1；

    4.3.否则，将s1栈顶的运算符弹出并压入到s2中，再次转到(4.1)与s1中新的栈顶运算符相比较；

  5. 遇到括号时：
    (1) 如果是左括号“ ( ”，则直接压入s1
    (2) 如果是右括号“ ) ”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃

  6. 重复步骤2至5，直到表达式的最右边

  7. 将s1中剩余的运算符依次弹出并压入s2

  8. 依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

注：中缀表达式转为前缀表达式是从又往左扫描中缀表达式，核心算法思想相同😄😄

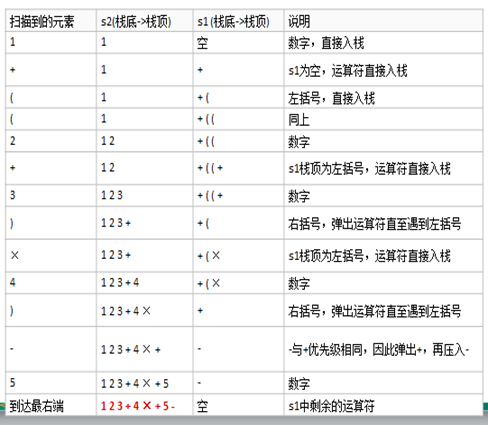
实例分析

将中缀表达式1+((2+3)*4)-5转换为前缀表达式。

按照步骤最终结果为：1 2 3 + 4 * + 5 -

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
//1、编写一个类 Operation 可以返回一个运算符 对应的优先级
class Operation {
    //写一个方法，返回对应的优先级数字
    public static int getValue(String operation) {
        int result = 0;
        int ADD = 1;
        int SUB = 1;
        int MUL = 2;
        int DIV = 2;
        switch (operation) {
            case "+":
                result = ADD;
                break;
            case "-":
                result = SUB;
                break;
            case "*":
                result = MUL;
                break;
            case "/":
                result = DIV;
                break;
            default:
                System.out.println("不存在该运算符" + operation);
                break;
        }
        return result;
    }
}

//2、因为直接对str进行操作，不方便，因此，
//先将“1+((2+3)*4)-5”=》中缀的表达式对应的List
// 即“1+((2+3)*4)-5” =》 ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]
//将中缀表达式转成对应的List
public static List<String> toInfixExpression(String s) {
    //定义一个List,存放中缀表达式对应的内容
    List<String> ls = new ArrayList<String>();
    int i = 0; //这是一个指针，用于遍历 中缀表达式字符串
    String str; //对多位数的拼接
    char c; //每遍历到一个字符，就放入到c
    do {
        //如果c是一个非数字，需要加入到ls
        if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) {
            ls.add("" + c);
            i++;
        } else {
            //如果是一个数，需要考虑多位数
            str = ""; // 先将str 置成""
            while (i < s.length() && (c = s.charAt(i)) >= 48 
                   && (c = s.charAt(i)) <= 57) {
                str += c; //拼接
                i++;
            }
            ls.add(str);
        }
    }while (i < s.length());

    //返回中缀表达式的list
    return ls;
}

//3、将得到的中缀表达式对应的List转换为后缀表达式对应的List
//即ArrayList[1,+,(,(,2,+,3,),*,4,),-,5] =》ArrayList[1,2,3,+,4,*,+,5,-]
public static List<String> parseSuffixExpressionList(List<String> ls) {
        //定义两个栈
        Stack<String> s1 = new Stack<String>(); //符号栈
        //说明:s2这个栈,在整个转换过程中，没有pop操作，而且后面还需要逆序输出
        //因此比较麻烦，这里我们就不用 Stack<String> 直接使用List<String> s2
        //Stack<String> s2 = new Stack<String>(); // 储存中间结果的栈s2
        List<String> s2 = new ArrayList<String>(); // 储存中间结果的Lists2

        //遍历ls
        for (String item : ls) {
            //如果是一个数，则加入到s2
            if (item.matches("\\d+")) {
                s2.add(item);
            } else if (item.equals("(")) {
                s1.push(item);
            } else if (item.equals(")")) {
                //如果是右括号“ ) ”，则依次弹出s1栈顶的运算符，并压入s2
                //直到遇到左括号为止，此时将这一对括号丢弃
                while (!s1.peek().equals("(")) {
                    s2.add(s1.pop());
                }
                s1.pop(); //消除小括号
            } else {
                //当item的优先级小于等于s1栈顶运算符, 
                //将s1栈顶的运算符弹出并加入到s2中，
                //再次转到(4.1)与s1中新的栈顶运算符相比较
                //问题：我们缺少一个比较优先级高低的方法
                while(s1.size() != 0 && Operation.getValue(s1.peek())
                      >= Operation.getValue(item) ) {
                    s2.add(s1.pop());
                }
                //还需要将item压入栈
                s1.push(item);
            }
        }

        //将s1中剩余的运算符依次弹出并加入s2
        while(s1.size() != 0) {
            s2.add(s1.pop());
        }
    	//注意因为是存放到List, 
    	//因此按顺序输出就是对应的后缀表达式对应的List
        return s2; 
    }

然后结合着后缀表达式的求值，便可实现完整的逆波兰计算器！📅📅

加油😘😘

北以晨光 wechat
欢迎您扫一扫上面的微信公众号，订阅我的博客！
------ 本文结束感谢您的阅读 ------
相关文章