0%

数据结构-线性表（一）概念及基本操作

发表于 更新于 分类于
本文字数： 8.6k 阅读时长 ≈ 8 分钟

数据结构

线性表（一）概念及基本操作

思维导图

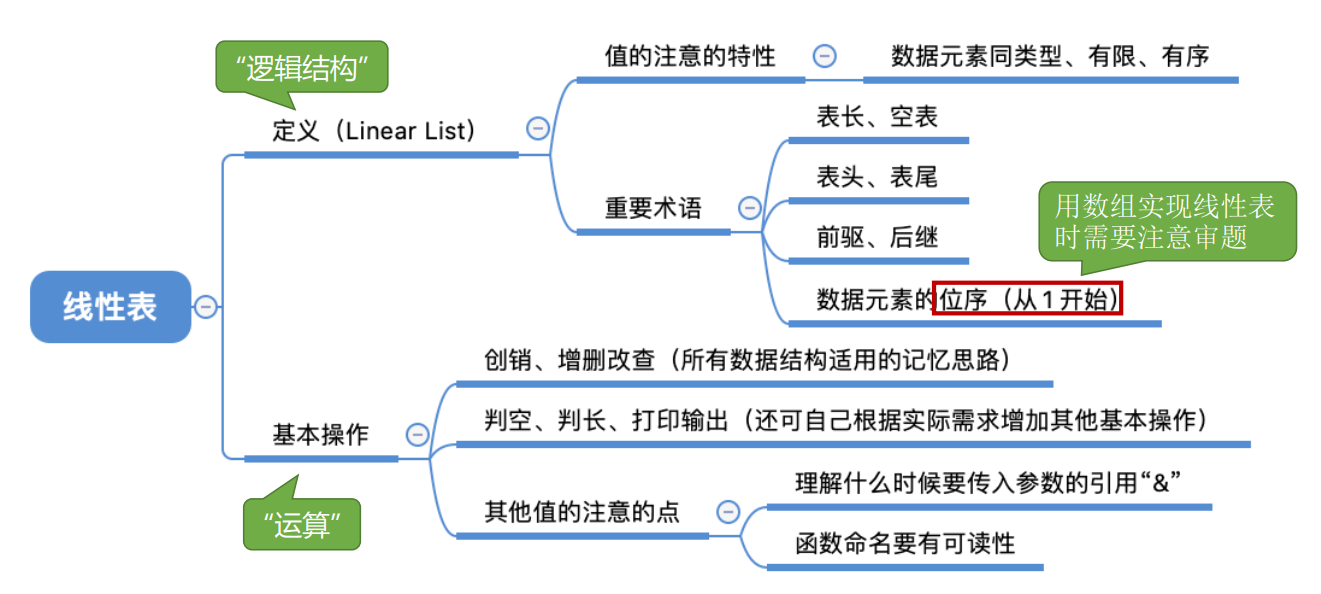
2.1 线性表的定义及基本操作

2.1.1 定义

线性表是具有相同数据类型的n（n≥0）个数据元素的有限序列，其中n为表长，当n = 0时线性表是一个空表。若用L命名线性表，则其一般表示为

$L = (a_1, a_2, … , a_i, a_i+1, … , a_n)$

几个概念：
$a_i$是线性表中的“第i个”元素线性表中的位序
$a_1$是表头元素；$a_n$是表尾元素。
除第一个元素外，每个元素有且仅有一个直接前驱；除最后一个元素外，每个元素有且仅有一个直接后继 。

2.1.2 基本操作

InitList(&L)：初始化表。构造一个空的线性表L，分配内存空间。

DestroyList(&L)：销毁操作。销毁线性表，并释放线性表L所占用的内存空间。

ListInsert(&L,i,e)：插入操作。在表L中的第i个位置上插入指定元素e。

ListDelete(&L,i,&e)：删除操作。删除表L中第i个位置的元素，并用e返回删除元素的值。

LocateElem(L,e)：按值查找操作。在表L中查找具有给定关键字值的元素。

GetElem(L,i)：按位查找操作。获取表L中第i个位置的元素的值。

其他常用操作：

Length(L)：求表长。返回线性表L的长度，即L中数据元素的个数。

PrintList(L)：输出操作。按前后顺序输出线性表L的所有元素值。

Empty(L)：判空操作。若L为空表，则返回true，否则返回false。

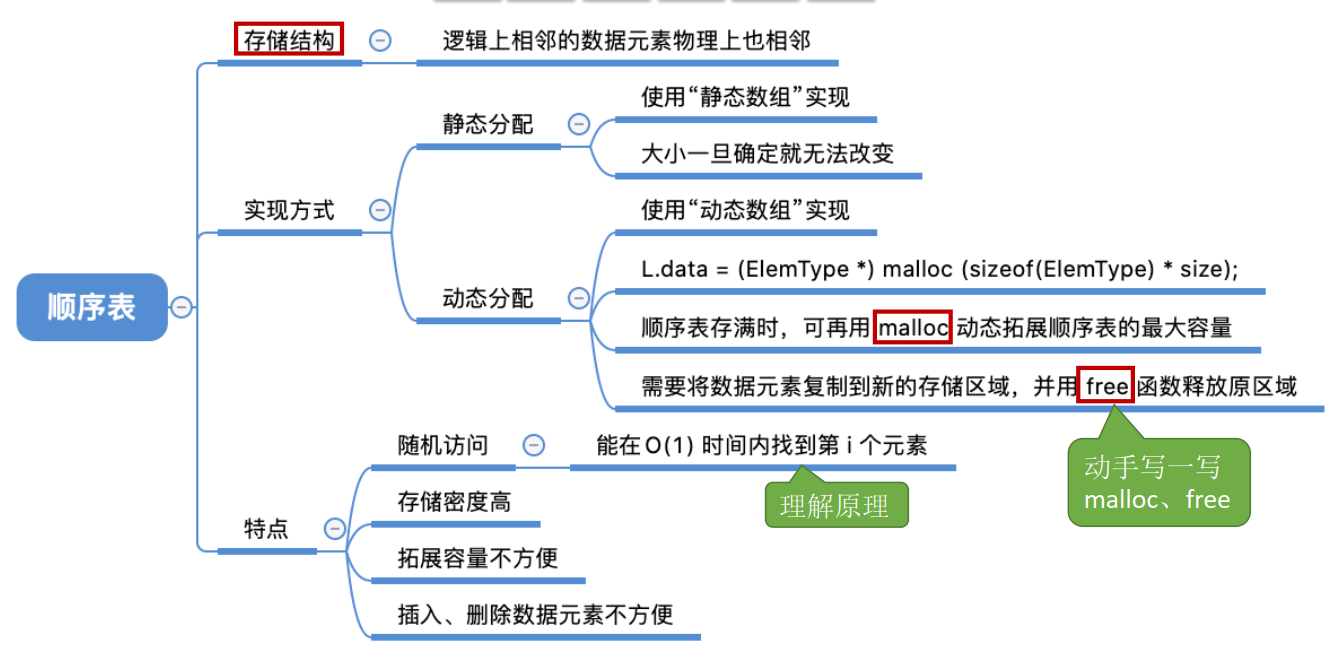
2.2 线性表的顺序表示

2.2.1 定义

定义： 顺序表–用顺序存储的方式实现线性表顺序存储。把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中，元素之间的关系由存储单元的邻接关系来体现。

1、静态分配

给各个数据元素分配连续的存储空间，大小为MaxSize x sizeof(ElemType) 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <stdio.h>
#define MaxSize 10 //定义最大长度
typedef struct SqList
{
    /* data */
    int data[MaxSize]; //用静态的“数组”存放数据元素
    int length;        //顺序表的当前长度
};

void InitList(SqList &L)
{
    L.length = 0; //顺序表初始长度为0；
}

int main()
{
    SqList L; //声明一个顺序表
    InitList(L); //初始化
    for (int i = 0; i < L.length; i++)
    {
        /* code */
        printf("data[%d]=%d\n", i, L.data[i]);
    }
    return 0;
}

2、动态分配

C语言知识

1、malloc 是一个系统函数，它是 memory allocate 的缩写。其中memory是“内存”的意思，allocate是“分配”的意思。顾名思义 malloc 函数的功能

就是“分配内存”。要调用它必须要包含头文件<stdlib.h>。

malloc 函数的返回值是一个地址，这个地址就是动态分配的内存空间的起始地址。如果此函数未能成功地执行，如内存空间不足，则返回空指针

NULL。

1
int *p = (int *)malloc(4);

请求系统分配 4 字节的内存空间，并返回第一字节的地址，然后赋给指针变量 p。当用 malloc 分配动态内存之后，上面这个指针变量 p 就被初始

化了。

2、sizeof(x) 计算变量x的长度。

1
int *p = malloc(sizeof(int));

sizeof（int）的值是 int 型变量所占的字节数，这样就能很好地表示当前计算机中 int 型变量占几字节。这样写程序的可移植性就增强了。所以动态

内存最好是需要多少就构建多少。

3、free(p) 释放指针p所指变量的存储空间，即彻底删除一个变量

前面定义了一个指向动态内存的指针变量 p：

1
int *p = malloc(sizeof*(int));

前面讲过，动态分配的内存空间是由程序员手动编程释放的。那么怎么释放呢？用 free 函数。

free 函数无返回值，它的功能是释放指针变量 p 所指向的内存单元。此时 p 所指向的那块内存单元将会被释放并还给操作系统，不再归它使用。

操作系统可以重新将它分配给其他变量使用。

需要注意的是，释放并不是指清空内存空间，而是指将该内存空间标记为“可用”状态，使操作系统在分配内存时可以将它重新分配给其他变量使用。

注意：

只有动态创建的内存才能用 free 把它释放掉，静态内存是不能用free释放的。静态内存只能由系统释放。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <stdio.h>
#include <stdlib.h>
#define InitSize 10 //顺序表的初始长度
typedef struct SqList
{
    /* data */
    int *data; //用静态的“数组”存放数据元素
    int MaxSize; //定义最大长度
    int length; //顺序表的当前长度
};

void InitList(SqList &L)
{
    //用malloc函数申请一片连续的存储空间
    L.data = (int *)malloc(InitSize*sizeof(int));
    L.length = 0;
    L.MaxSize = InitSize;
}

void IncreaseSize(SqList &L, int len) {
    int *p = L.data;
    L.data = (int *)malloc((L.MaxSize + len)*sizeof(int));
    for (int i = 0; i < L.length; i++)
    {
        /* code */
        L.data[i] = p[i];  //将数据复制到新区域
    }
    L.MaxSize = L.MaxSize + len; //顺序表最大长度增加len
    free(p);  //释放原来的内存空间
    
}

int main()
{
    SqList L;    //声明一个顺序表
    InitList(L); //初始化
    //插入元素
    
    IncreaseSize(L, 5);
    return 0;
}

3、顺序表特点

  1. 随机访问，即可以在 O(1) 时间内找到第 i 个元素。（代码实现：data[i-1];静态分配、动态分配都一样 ）
  2. 存储密度高，每个节点只存储数据元素
  3. 拓展容量不方便（即便采用动态分配的方式实现，拓展长度的时间复杂度也比较高）
  4. 插入、删除操作不方便，需要移动大量元素

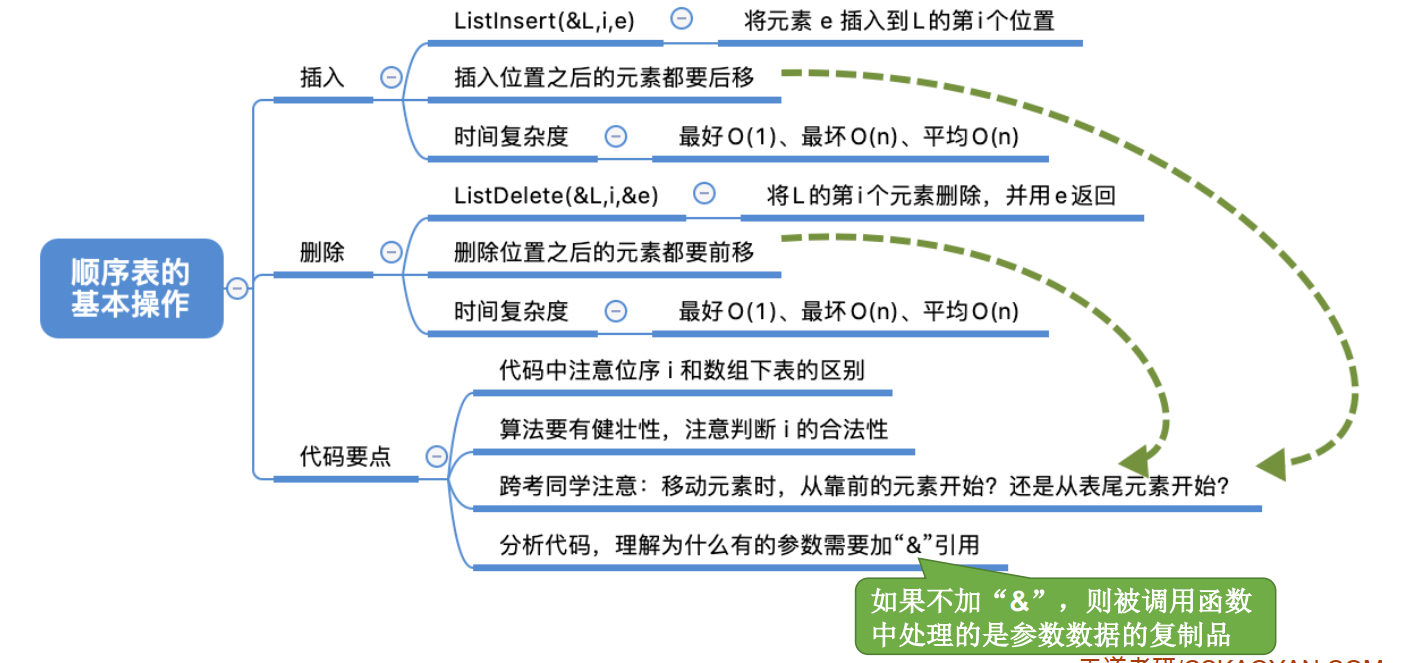
2.2.2 基本操作的实现

1、插入

ListInsert(&L,i,e)：插入操作。在表L中的第i个位置上插入指定元素e。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include<stdio.h>
#include<iostream>
#define MaxSize 10
using namespace std;
typedef struct
{
    /* data */
    int data[MaxSize];
    int length;
}SqList;

/**
 * 初始化
 */
void InitList(SqList &L)
{
    L.length = 0; //顺序表初始长度为0；
}

/**
 * 插入顺序表
 */
bool ListInsert(SqList &L, int i, int e) {
    //判断i的范围是否有效
    if (i < 1 || i > L.length + 1)
    {
        return false;
        /* code */
    }
    //判断当前存储空间是否已满，不能插入
    if (L.length >= MaxSize) 
    {
        /* code */
        return false;

    }
    //将第i个元素及以后的元素后移
    for (int j = L.length; j >= i; j--)
    {
        /* code */
        L.data[j] = L.data[j - 1];
    }
    //在位置i处放入e
    L.data[i - 1] = e;
    L.length++;  //长度++
    return true;
    
}

/**
 * 打印输出
 */ 
void printList(SqList L) {
    cout << "长度length = " << L.length << endl;
    cout << "数据为：" << endl;
    for (int i = 0; i < L.length; i++)
    {
        /* code */
        cout << "data[" << i << "] = " << L.data[i] << endl;
        
    }
    
}
int main() {
    SqList L;
    InitList(L);
    //赋值
    for (int i = 0; i < 5; i++)
    {
        /* code */
        L.data[i] = i;
        L.length++;
    }
    printList(L);
    bool flag = ListInsert(L, 2, 6);
    cout << flag << endl;
    printList(L);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
长度length = 5
数据为：
data[0] = 0
data[1] = 1
data[2] = 2
data[3] = 3
data[4] = 4
1
长度length = 6
数据为：
data[0] = 0
data[1] = 6
data[2] = 1
data[3] = 2
data[4] = 3
data[5] = 4

时间复杂度

(1)最好情况：新元素插入到表尾，不需要移动元素

i = n+1，循环0次；最好时间复杂度 = O(1)

(2)最坏情况：新元素插入到表头，需要将原有的 n 个元素全都向后移动

i = 1，循环 n 次；最坏时间复杂度 = O(n);

(3)平均情况：假设新元素插入到任何一个位置的概率相同，即 i = 1,2,3, … , length+1 的概率都是 p = 1/(n+1)

i = 1，循环 n 次；i = 2 时，循环 n - 1 次；i = 3，循环 n-2 次 …… i = n + 1时，循环0次

$平均循环次数 = np + (n-1)p + (n-2)p + …… + 1⋅p = \frac{n(n+1)}{2} * \frac{1}{(n+1)} = \frac{n}{2}$

平均时间复杂度 = O(n)

2、删除

ListDelete(&L,i,&e)：删除操作。删除表L中第i个位置的元素，并用e返回删除元素的值。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<stdio.h>
#include<iostream>
#define MaxSize 10
using namespace std;
typedef struct
{
    /* data */
    int data[MaxSize];
    int length;
}SqList;

/**
 * 初始化
 */
void InitList(SqList &L)
{
    L.length = 0; //顺序表初始长度为0；
}

/**
 * 删除顺序表
 */
bool ListDelete(SqList &L, int i, int &e) {
    //判断i的范围是否有效
    if (i < 1 || i > L.length + 1)
    {
        return false;
        /* code */
    }
    e = L.data[i - 1];
    //将第i个元素及以后的元素前移
    for (int j = i; j < L.length; j++)
    {
        /* code */
        L.data[j - 1] = L.data[j];
    }
    L.length--;  //长度--
    return true;
    
}

/**
 * 打印输出
 */ 
void printList(SqList L) {
    cout << "长度length = " << L.length << endl;
    cout << "数据为：" << endl;
    for (int i = 0; i < L.length; i++)
    {
        /* code */
        cout << "data[" << i << "] = " << L.data[i] << endl;
        
    }
    
}
int main() {
    SqList L;
    InitList(L);
    //赋值
    for (int i = 0; i < 5; i++)
    {
        /* code */
        L.data[i] = i;
        L.length++;
    }
    int e;
    printList(L);
    ListDelete(L, 4, e);
    printList(L);
    cout << "删除的数字为 " << e << " " << endl;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
长度length = 5
数据为：
data[0] = 0
data[1] = 1
data[2] = 2
data[3] = 3
data[4] = 4
长度length = 4
数据为：
data[0] = 0
data[1] = 1
data[2] = 2
data[3] = 4
删除的数字为 3

时间复杂度

(1)最好情况：删除表尾元素，不需要移动其他元素

i = n，循环 0 次；最好时间复杂度 = O(1)

(2)最坏情况：删除表头元素，需要将后续的 n-1 个元素全都向前移动

i = 1，循环 n-1 次；最坏时间复杂度 = O(n);

(3)平均情况：假设删除任何一个元素的概率相同，即 i = 1,2,3, … , length 的概率都是 $p = \frac{1}{n}$

i = 1，循环 n-1 次；i=2 时，循环 n-2 次；i=3，循环 n-3 次 …… i =n 时，循环0次

$平均循环次数 = (n-1)p + (n-2)p + …… + 1⋅p = \frac{n(n-1)}{2} * \frac{1}{n} = \frac{(n-1)}{2}$

平均时间复杂度 = O(n)

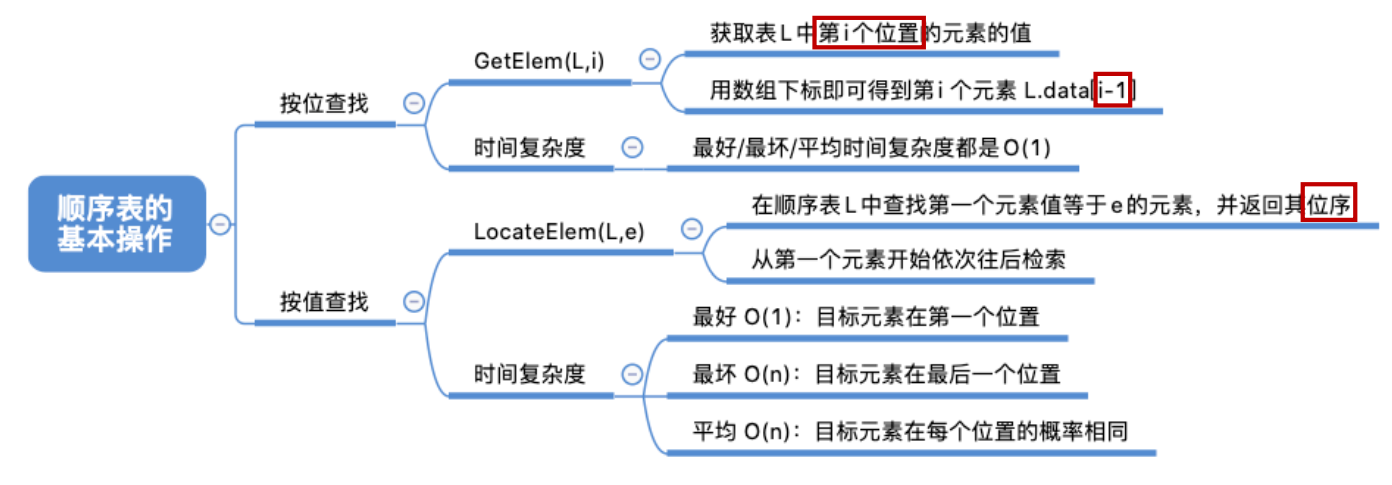
3、查找

（1）按位查找

GetElem(L,i)：按位查找操作。获取表L中第i个位置的元素的值。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#define InitSize 10
using namespace std;
typedef struct
{
    /* data */
    int *data; //动态分配
    int length;
    int MaxSize;
} SqList;

/**
 * 初始化
 */
void InitList(SqList &L)
{
    L.data = (int *)malloc(InitSize*sizeof(int));
    L.MaxSize = InitSize;
    L.length = 0; //顺序表初始长度为0；
}

/**
 * 按位查找顺序表
 */
int ListSearchBySite(SqList L,  int i)
{
    cout << "查找第 " << i << " 位的值为：";
    return  L.data[i - 1];
}

/**
 * 打印输出
 */
void printList(SqList L)
{
    cout << "长度length = " << L.length << endl;
    cout << "数据为：" << endl;
    for (int i = 0; i < L.length; i++)
    {
        /* code */
        cout << "data[" << i << "] = " << L.data[i] << endl;
    }
}

int main()
{
    SqList L;
    InitList(L);
    //赋值
    for (int i = 0; i < 5; i++)
    {
        /* code */
        L.data[i] = i;
        L.length++;
    }
    printList(L);
    cout << ListSearchBySite(L, 3) << endl;
    return 0;
}
1
2
3
4
5
6
7
8
长度length = 5
数据为：
data[0] = 0
data[1] = 1
data[2] = 2
data[3] = 3
data[4] = 4
查找第 3 位的值为：2

时间复杂度

由于顺序表的各个数据元素在内存中连续存放，因此可以根据起始地址和数据元素大小立即找到第 i 个元素——“随机存取”特性

时间复杂度 = O(n)

（2）按值查找

LocateElem(L,e)：按值查找操作。在表L中查找具有给定关键字值的元素。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#define InitSize 10
using namespace std;
typedef struct
{
    /* data */
    int *data;
    int length;
    int MaxSize;
} SqList;

/**
 * 初始化
 */
void InitList(SqList &L)
{
    L.data = (int *)malloc(InitSize * sizeof(int));
    L.MaxSize = InitSize;
    L.length = 0; //顺序表初始长度为0；
}

/**
 * 按值查找顺序表
 */
int ListSearchByValue(SqList L, int e)
{
    cout << "查找值为 " << e << " 的位置为：";
    for (int i = 0; i < L.length; i++)
        if (L.data[i] == e)
            return i + 1; //数组下标为i的元素值等于e，返回其位序i+1
    return 0;             //退出循环，说明查找失败
}


/**
 * 打印输出
 */
void printList(SqList L)
{
    cout << "长度length = " << L.length << endl;
    cout << "数据为：" << endl;
    for (int i = 0; i < L.length; i++)
    {
        /* code */
        cout << "data[" << i << "] = " << L.data[i] << endl;
    }
}

int main()
{
    SqList L;
    InitList(L);
    //赋值
    for (int i = 0; i < 5; i++)
    {
        /* code */
        L.data[i] = i;
        L.length++;
    }
    printList(L);
    cout << ListSearchByValue(L, 1) << endl;
    return 0;
}
1
2
3
4
5
6
7
8
长度length = 5
数据为：
data[0] = 0
data[1] = 1
data[2] = 2
data[3] = 3
data[4] = 4
查找值为 1 的位置为：2

时间复杂度

（1）最好情况：目标元素在表头循环1次；最好时间复杂度 = O(1);

（2）最坏情况：目标元素在表尾循环 n 次；最坏时间复杂度 = O(n);

（3）平均情况：假设目标元素出现在任何一个位置的概率相同，都是 $\frac{1}{n}$

$平均循环次数 = np + (n-1)p + (n-2)p + …… + 1⋅p = \frac{n(n+1)}{2} * \frac{1}{n} = \frac{(n+1)}{2}$

平均时间复杂度 = O(n)

北以晨光 wechat
欢迎您扫一扫上面的微信公众号，订阅我的博客！
------ 本文结束感谢您的阅读 ------
相关文章