数据结构

线性表（三）双链表

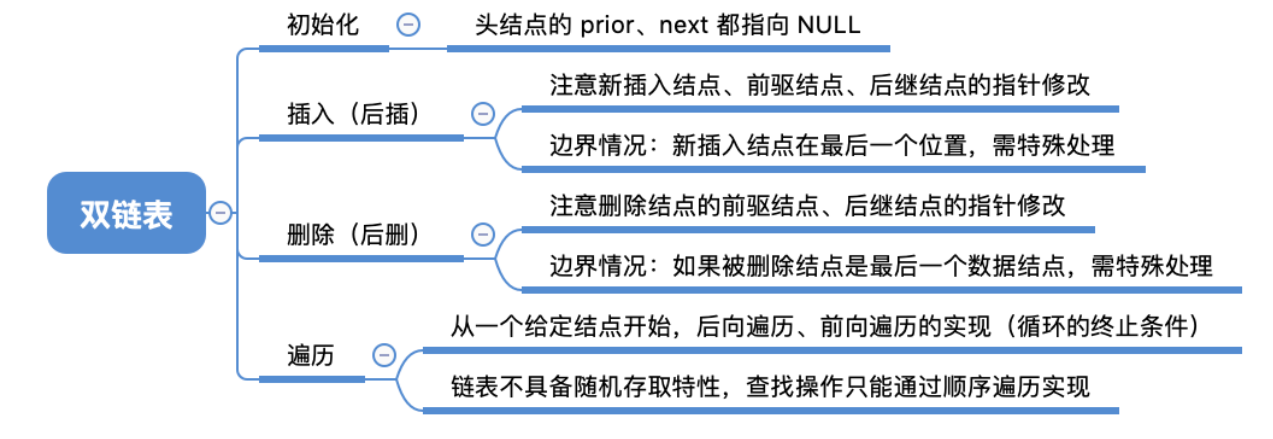
思维导图

2.1 线性表的链式表示

链式存储线性表时，不需要使用地址连续的存储单元，结点在存储器中的位置是任意的，即逻辑上相邻的数据元素在物理上不一定相邻。

2.2 双链表

1、定义

比单链表多一个 前驱指针prior

优缺点：

可进可退，存储密度比单链表更低一点；

双链表不可随机存取；

按位查找、按值查找操作都只能用遍历的方式实现。

时间复杂度O(n)

2、基本操作

（1）插入

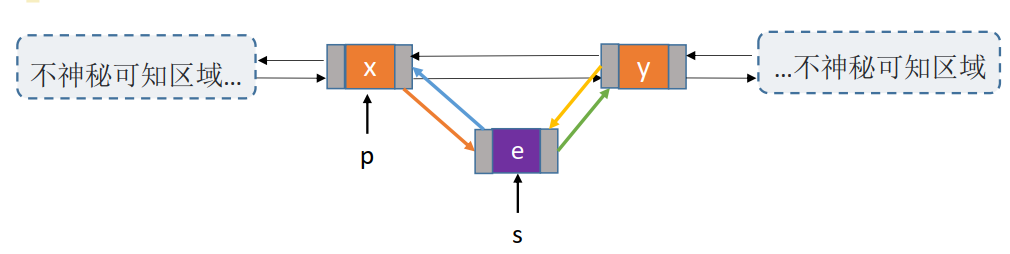
（2）删除

（3）遍历

👉 遍历方式和单链表一样，可以向前遍历也可以向后遍历

（4）代码

#include<iostream>
#include<stdlib.h>
#include<stdio.h>
using namespace std;

typedef struct DoubleLinkedList
{
    /* data */
    int data;
    DoubleLinkedList *prior, *next;
}DNode, *DLinkList;

/**
 * 初始化
 */ 
bool InitDLinkList(DLinkList &L) {
    L = (DNode *)malloc(sizeof(DNode));
    if(L == NULL)
        return false;
    L->prior = NULL;
    L->next = NULL;
    return true;
}

//判断双链表是否为空
bool isEmpty(DLinkList L) {
    return(L->next == NULL);
}

/**
 * 插入数据
 */ 
bool InsertNode(DLinkList &L, int e) {
    DNode *s;
    DNode *temp = L;
    while (temp->next != NULL)
    {
        /* code */
        temp = temp->next;
    }
    s = (DNode *)malloc(sizeof(DNode));
    s->data = e;
    s->next = temp->next;
    if (temp->next != NULL)
    {
        temp->next->prior = s;
    }
    s->prior = temp;
    temp->next = s;
    
    cout << "插入成功！" << endl;
    return true;
    
}

/**
 * 后向遍历数据
 */
void printNodetoNext(DLinkList L) {
    cout << "后向遍历" << endl;
    DNode *p = L->next;
    while(p != NULL) {
        cout << p->data << endl;
        p = p->next;
    }
}

/**
 * 前向遍历数据
 */
void printNodetoPrior(DLinkList L)
{
    cout << "前向遍历" << endl;
    DNode *p = L;
    while (p->prior != NULL)
    {
        cout << p->data << endl;
        p = p->prior;
    }
}

/**
 * 删除指定位置元素
 */ 
bool DeleteNode(DLinkList &L, int i) {
   DNode *p = L;
   int j = 0;
   while(j < i - 1) {
       p = p->next;
       j++;
   } 
   DNode *q = p->next;
   p->next = q->next;
   if(q->next != NULL) {
       q->next->prior = p;
   }
   free(q);
   cout << "删除成功！" << endl;
   return true;
}

int main() {
    //
    DLinkList L;
    InitDLinkList(L);
    cout << isEmpty(L) << endl;
    //插入数据
    InsertNode(L, 4);
    InsertNode(L, 2);
    InsertNode(L, 5);
    InsertNode(L, 8);
    //
    printNodetoNext(L);
    //
    DeleteNode(L, 2);
    printNodetoNext(L);
    return 0;
}

1
插入成功！
插入成功！
插入成功！
插入成功！
后向遍历
4
2
5
8
删除成功！
后向遍历
4
5
8