数据结构-树和二叉树(七)哈夫曼树📑
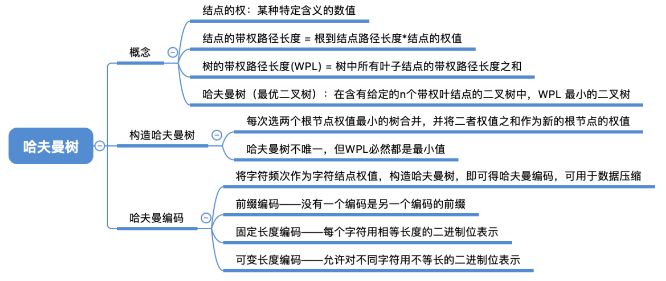
1、定义
结点的权:有某种现实含义的数值(如:表示结点的重要性等)
结点的带权路径长度: 从树的根到该结点的路径长度(经过的边数)与该结点上权值的乘积
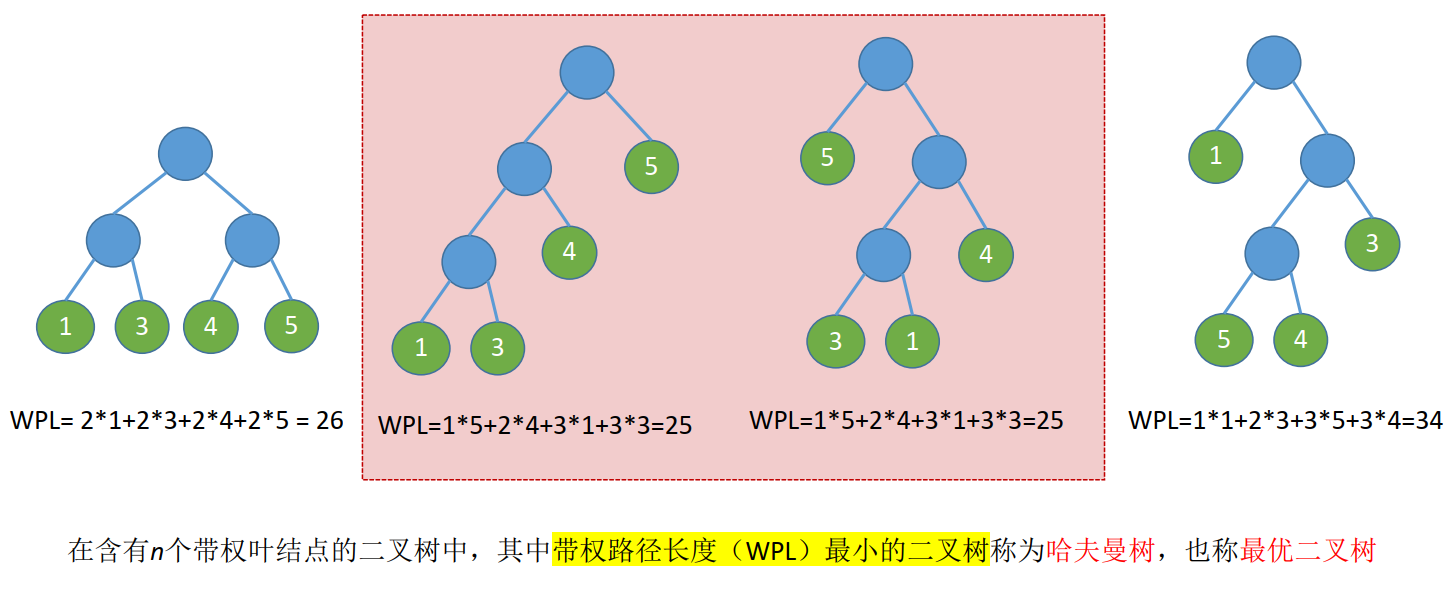
树的带权路径长度: 树中所有叶结点的带权路径长度之和(WPL, Weighted Path Length)
$$
WPL = \sum_{i=1}^{100}w_{i}l_{i}
$$
其中,wi是第 i 个叶节点所带的全值,li是该叶节点到根结点的路径长度。
2、构造
给定n个权值分别为w
1, w2,…, wn的结点,构造哈夫曼树的算法描述如下:
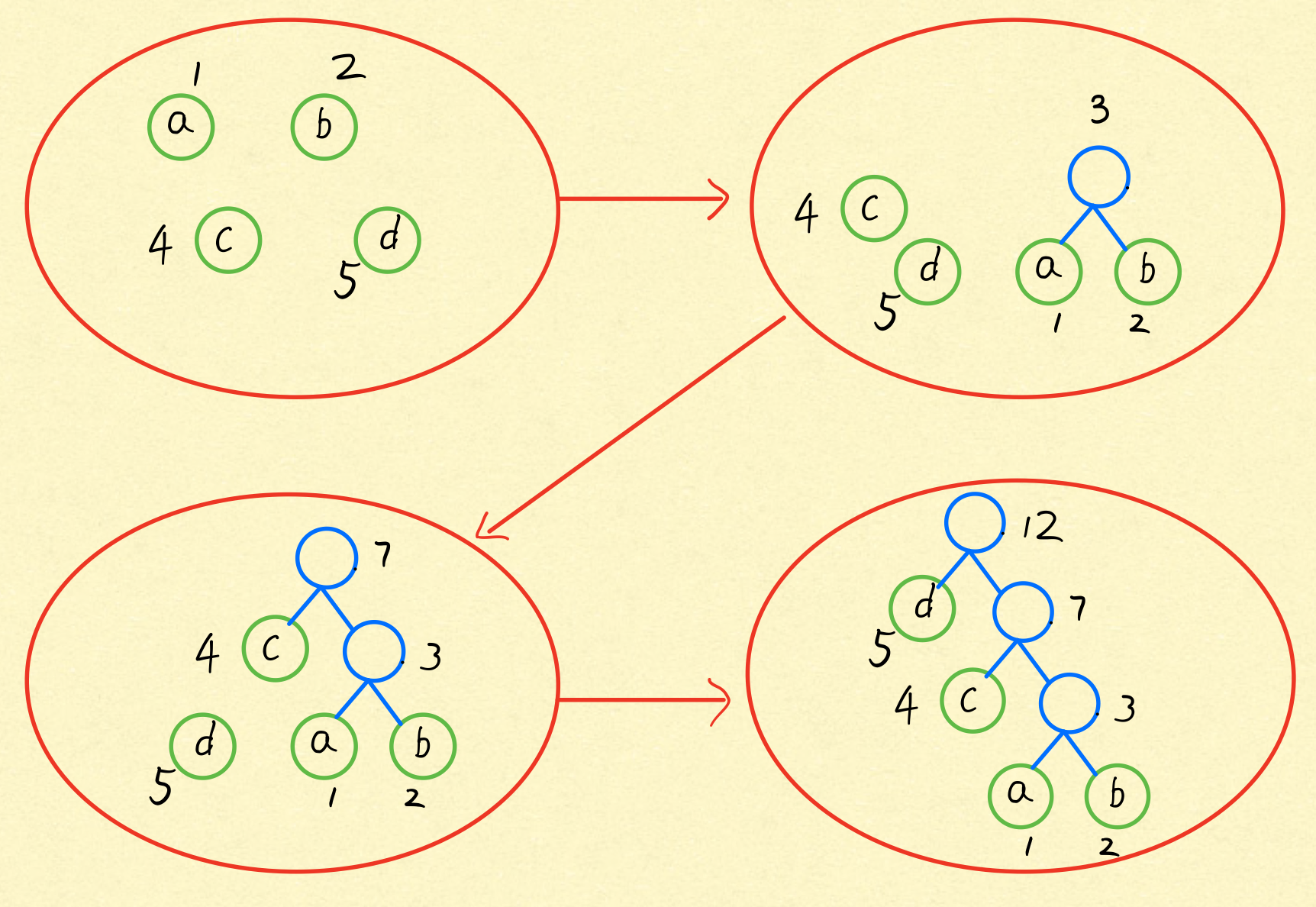
将这n个结点分别作为n棵仅含一个结点的二叉树,构成森林F。
构造一个新结点,从F中选取两棵根结点权值最小的树作为新结点的左、右子树,
并且将新结点的权值置为左、右子树上根结点的权值之和。
从F中删除刚才选出的两棵树,同时将新得到的树加入F中。
重复步骤2)和3),直至F中只剩下一棵树为止。
==特点:==
- 每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越大
- 叶节点为n,哈夫曼树的结点总数为2n - 1。
- 哈夫曼树中不存在度为1的结点。
- 哈夫曼树并不唯一,但WPL必然相同且为最优
3、哈夫曼编码
固定长度编码——每个字符用相等长度的二进制位表示
可变长度编码——允许对不同字符用不等长的二进制位表示
若没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码
有哈夫曼树得到哈夫曼编码——字符集中的每个字符作为一个叶子结点,各个字符出现的频度作为结点的权值,根据之前介绍的方法构造哈夫曼树
🌰🌱(栗子)
某系统在通讯时,只出现C,A,S,T,B五种字符,其出现频率依次为2,4,2,3,3,试设计Huffman编码。
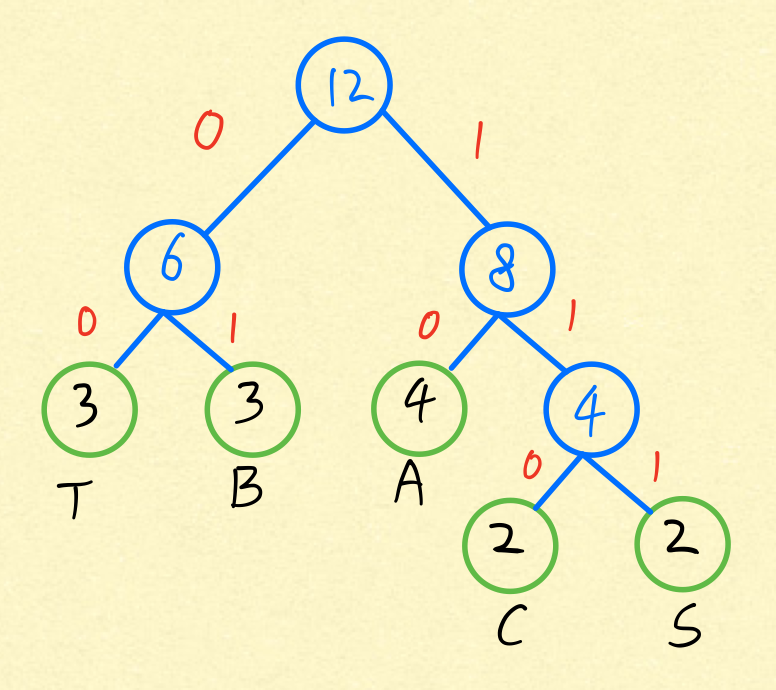
1、首先根据字符出现频率构造最优哈夫曼树,如图;
2、根据哈夫曼树,得出哈夫曼编码;
T 00
B 01
A 10
C 110
S 111
3、计算WPL
WPL = 2 * (3 + 3 + 4) + 3 * (2 + 2) = 32