数据结构-树和二叉树(六)二叉平衡树 ⚖
1、定义
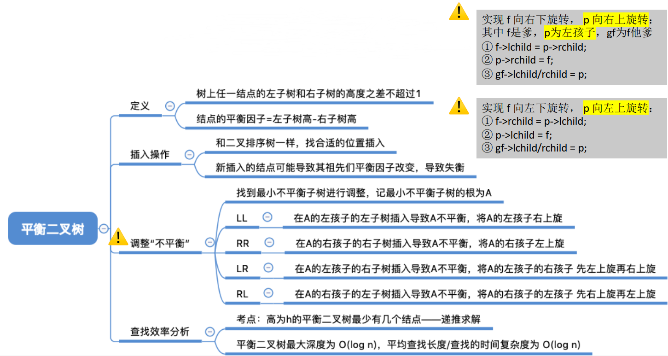
平衡二叉树(Balanced Binary Tree), 简称平衡树(AVL树) ——树上任一结点的左子树和右子树的高度之差不超过1。
结点的平衡因子 = 左子树高 - 右子树高。
2、AVL树的插入
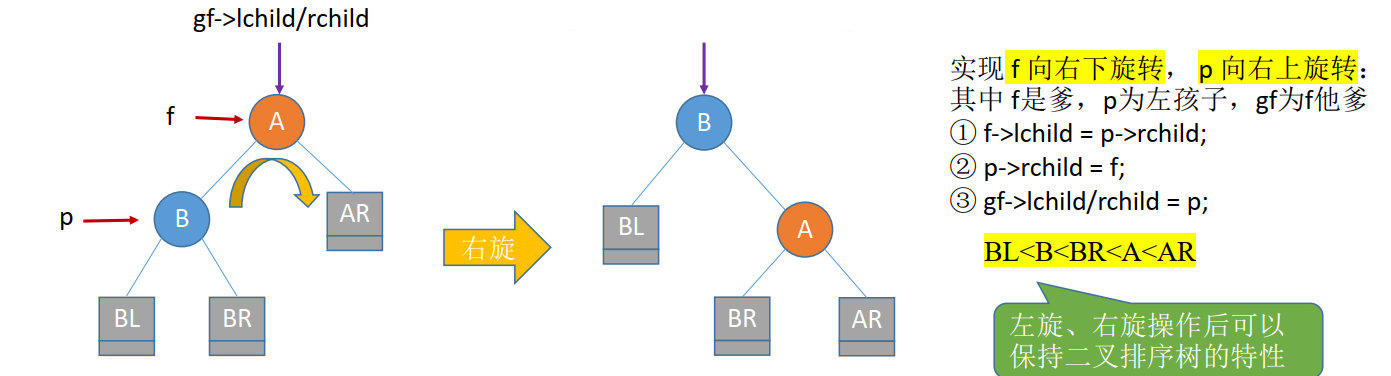
(1)LL平衡旋转
LL平衡旋转( 右单旋转)。由于在结点A的左孩子( L)的左子树( L)上插入了新结点, A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根结点,将A结点向右下旋转成为B的右子树的根结点,而B的原右子树则作为A结点的左子树。
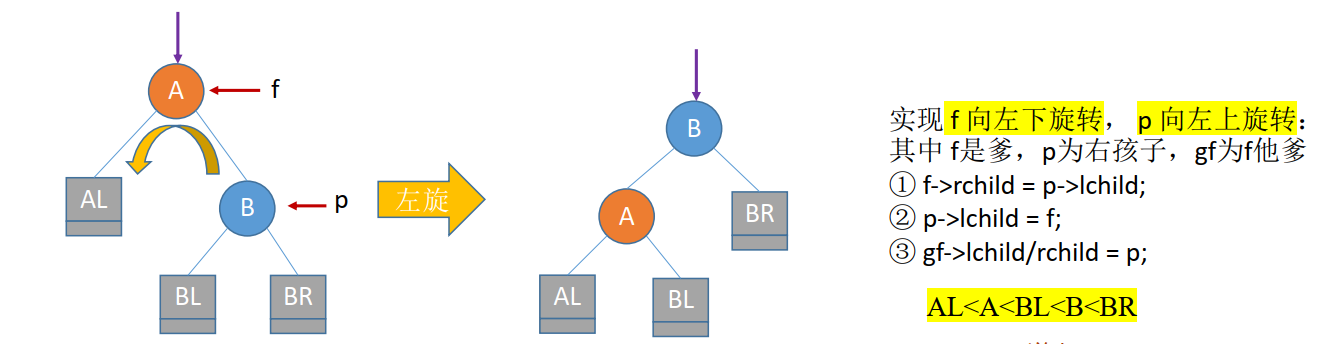
(2)RR平衡旋转
RR平衡旋转( 左单旋转)。由于在结点A的右孩子( R)的右子树( R)上插入了新结点, A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根结点,将A结点向左下旋转成为B的左子树的根结点,而B的原左子树则作为A结点的右子树。
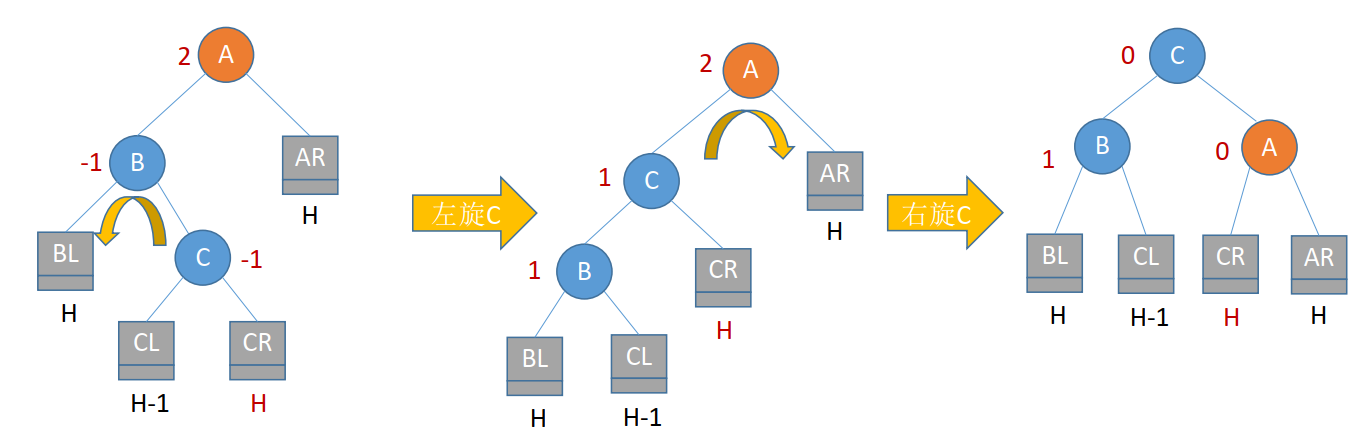
(3)LR平衡旋转
LR平衡旋转(先左后右双旋转)。由于在A的左孩子(L)的右子树(R)上插入新结点, A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要进行两次旋转操作,先左旋转后右旋转。先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置,然后再把该C结点向右上旋转提升到A结点的位置。
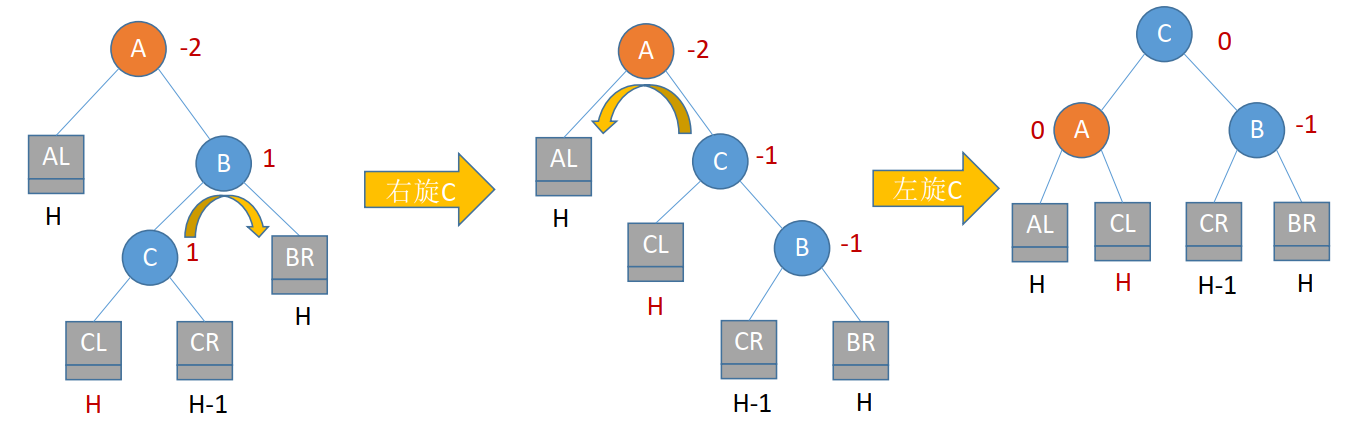
(4)RL平衡旋转
RL平衡旋转(先右后左双旋转)。由于在A的右孩子(R)的左子树(L)上插入新结点, A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要进行两次旋转操作,先右旋转后左旋转。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置,然后再把该C结点向左上旋转提升到A结点的位置。
3、查找效率分析
平衡二叉树—树上任一结点的左子树和右子树的高度之差不超过1
若树高为h,则最坏情况下,查找一个关键字最多需要对比 h 次,即查找操作的时间复杂度不可能超过 $O(h)$
假设以 n
h表示深度为 h 的平衡树中含有的最少结点数。则有$n_0 = 0, n_1 = 1, n_2 = 2,$ 并且有$n_h = n_{h-1} + n_{h-2} + 1 $
可以证明含有n个结点的平衡二叉树的最大深度为$O(log_2n)$ , 平衡二叉树的平均查找长度为$O(log_2n)$
4、例题
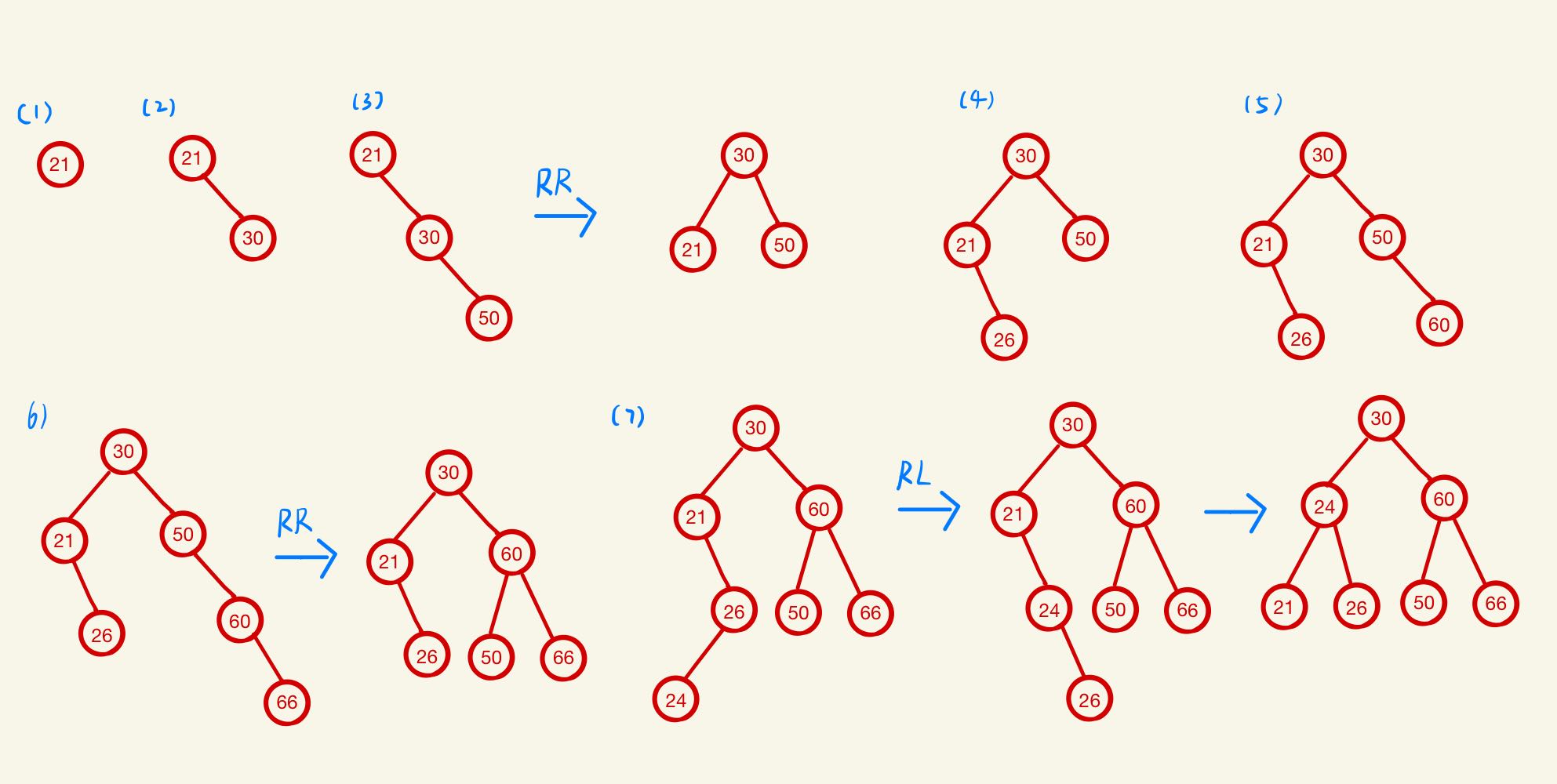
题目: 按顺序插入【21,30,50,26,60,66,24】构建平衡二叉树,请画出插入并调整为平衡二叉树的过程。
过程如下: